牛顿迭代法

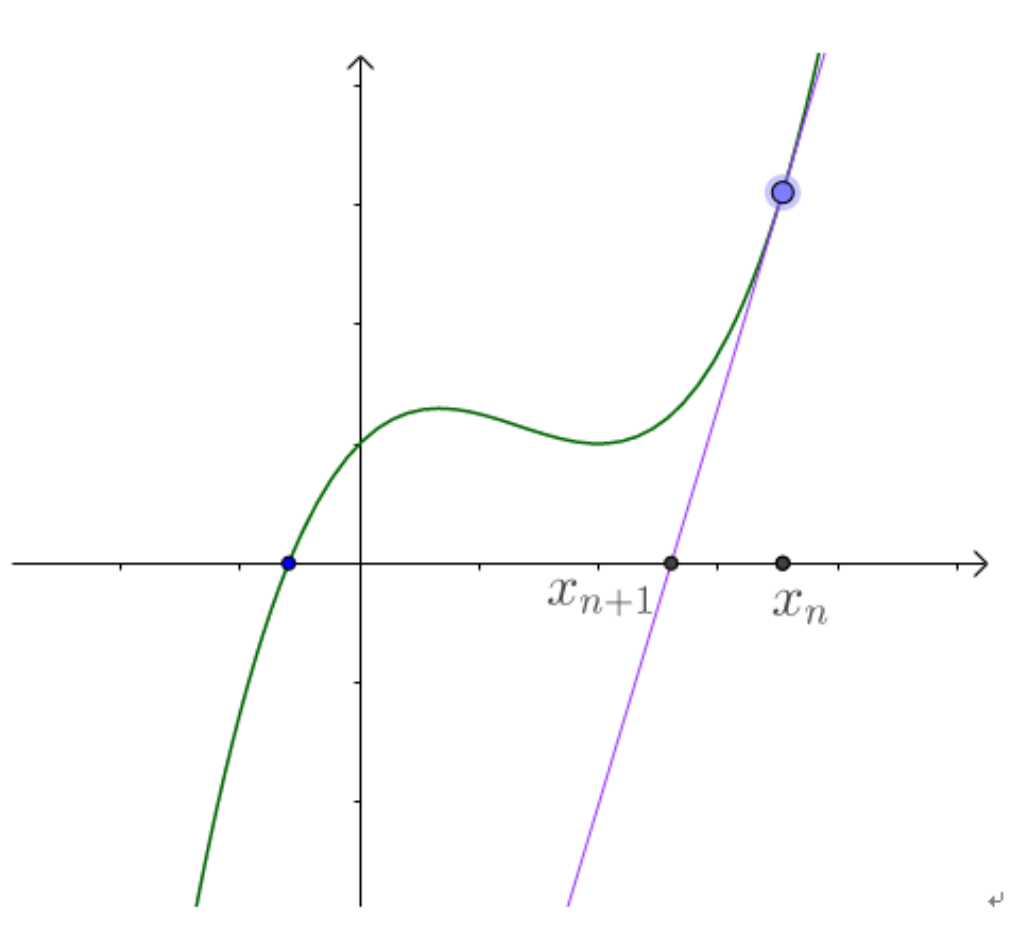
  • 如图，一条曲线$y=f(x)$，在$f(x_n)$处画一条切线交x轴于点$x_{n+1}$，接着在$f(x_{n+1})$处画切线交x轴于点$x_{n+2}$，继续……
  • 在这个过程中交点$x_{n+m}$会无限逼近曲线零点，即得到方程$f(x) = 0$的解。

求平方根

思路

  • 即求函数$f(x) = x^2 - n $的零点
  • 导函数$f^{’}(x) = 2x $
  • 在点$(x_n, x_n^2-n)$处的切线方程为$y - x_n^2 + n = 2x_n (x-x_n) $，即$y = 2x_nx - x_n^2 - n$
  • 则切线与x轴的交点$x_{n+1}$为$$\frac {x_n^2 - n} {2x_n}$$
  • 重复迭代直到得到精度满意的值

代码实现

package main

import (
	"fmt"
	"math"
)

func Sqrt(x float64) float64 {
	z := 1.0
	for math.Abs(z * z - x) > 1e-12 {
		z -= (z * z - x) / (2 * z)
	}
	return z
}

func main() {
	fmt.Println(Sqrt(2))
}

求k次方根

思路

  • $$x_{n+1} = x_{n} - \frac {f(x_n)} {f^{’}(x_n)}$$
  • $$x_{n+1} = x_n - \frac {x_n(1 - nx_n^{-k})} k$$

代码实现

package main

import (
	"fmt"
	"math"
)

func getRoot(x, k float64) float64 {
	z := 1.0
	for math.Abs(math.Pow(z, k) - x) > 1e-9 {
		z -= z * (1 - x * math.Pow(z, -k)) / k
	}
	return z
}

func main() {
	fmt.Println(getRoot(27, 3))
}

实现及其测试

// sqrt.go
package sqrt

import "errors"

const EPSILON = 1e-8

var ErrNegativeSqrt = errors.New("cannot Sqrt negative number")

type Float interface {
	float64 | float32
}

func abs[T Float](x T) T {
	if x < 0 {
		return -x
	}
	return x
}

func SqrtWithNR[T Float](num T) (T, error) {
	if num < 0 {
		return 0, ErrNegativeSqrt
	}
	z := T(1.0)
	for abs(z*z-num) > EPSILON {
		z -= (z*z - num) / (2 * z)
	}
	return z, nil
}

func SqrtWithBS[T Float](num T) (T, error) {
	if num < 0 {
		return 0, ErrNegativeSqrt
	}
	l, r := T(0.0), num
	for abs(l*l-num) > EPSILON {
		m := (l + r) / 2
		if m*m > num {
			r = m
		} else {
			l = m
		}
	}
	return l, nil
}

// sqrt_test.go
package sqrt_test

import (
	"math"
	"sqrt"
	"testing"
)

func TestSqrtWithNR(t *testing.T) {
	for i := 0; i < 10; i++ {
		num := float64(i)
		if z, err := sqrt.SqrtWithNR(num); err != nil {
			t.Error(err)
		} else if math.Abs(z*z-num) > sqrt.EPSILON {
			t.Errorf("%f != %f", z*z, num)
		}
	}
}

func TestSqrtWithBS(t *testing.T) {
	for i := 0; i < 10; i++ {
		num := float64(i)
		if z, err := sqrt.SqrtWithBS(num); err != nil {
			t.Error(err)
		} else if math.Abs(z*z-num) > sqrt.EPSILON {
			t.Errorf("%f != %f", z*z, num)
		}
	}
}

func BenchmarkSqrtWithNR(b *testing.B) {
	for i := 0; i < b.N; i++ {
		sqrt.SqrtWithNR(float64(i))
	}
}

func BenchmarkSqrtWithBS(b *testing.B) {
	for i := 0; i < b.N; i++ {
		sqrt.SqrtWithBS(float64(i))
	}
}

测试结果

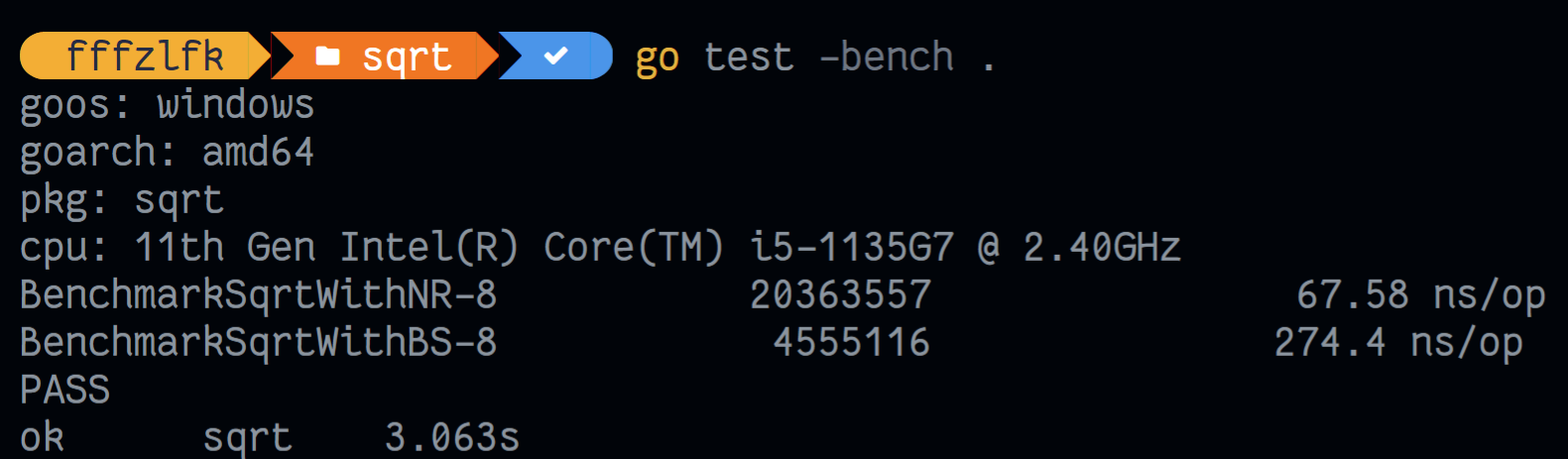
可以看出牛顿法相比于二分查找，性能要好！🥰