算法(第四版)
Union-Find
quickfind
Java implementation
public class QuickFindUF {
private int[] id;
private int count;
public QuickFindUF(int n) {
id = new int[n];
for (int i = 0; i < n; i++)
id[i] = i;
count = n;
}
public int count() {
return count;
}
public int find(int p) {
return id[p];
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public void union(int p, int q) {
int pid = find(p);
int qid = find(q);
if (pid != qid) {
for (int i = 0; i < id.length; i++)
if (id[i] == pid) {
id[i] = qid;
}
}
count--;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
QuickFindUF uf = new QuickFindUF(10);
while (in.hasNext()) {
int p = in.nextInt(), q = in.nextInt();
if (uf.connected(p, q)) continue;
uf.union(p, q);
}
}
}
analysis
The find() operation is certainly quick, as it only accesses the id[] array once in order to complete the operation. But quick-find is typically not useful for large problems because union() needs to scan through the whole id[] array for each input pair.
quick-union
implementation
import java.util.Scanner;
public class QuickUnionUF {
private int[] id;
private int count;
public QuickUnionUF(int n) {
id = new int[n];
for (int i = 0; i < n; i++)
id[i] = i;
count = n;
}
public int count() {
return count;
}
public int find(int p) {
while (p != id[p]) {
p = id[p];
}
return p;
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot != qRoot) {
id[pRoot] = qRoot;
} else return;
count--;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
QuickUnionUF uf = new QuickUnionUF(10);
while (in.hasNext()) {
int p = in.nextInt(), q = in.nextInt();
if (uf.connected(p, q)) continue;
uf.union(p, q);
}
}
}
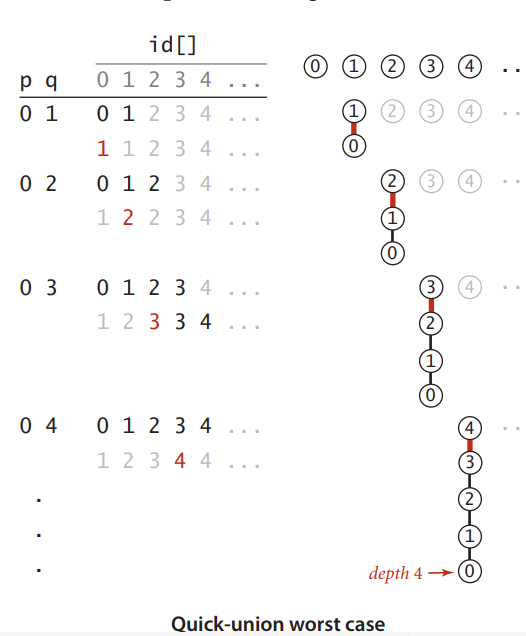
quick-union worst case
Weighted quick-union
import java.util.Scanner;
public class WeightedQuickUnionUF {
private int[] id;
private int[] sz;
private int count;
public WeightedQuickUnionUF(int N) {
count = N;
id = new int[N];
sz = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
}
for (int i = 0; i < N; i++)
sz[i] = 1;
}
public int find(int p) {
while (p != id[p]) {
id[p] = id[id[p]]; // path compression by halving
p = id[p];
}
return p;
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public void union(int p, int q) {
int i = find(p);
int j = find(q);
if (i == j) return;
if (sz[i] < sz[j]) {
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
count--;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
WeightedQuickUnionUF uf = new WeightedQuickUnionUF(10);
while (in.hasNext()) {
int p = in.nextInt(), q = in.nextInt();
if (uf.connected(p, q)) continue;
uf.union(p, q);
}
}
}
Performance characteristics of union-find algorithms
| algorithm | constructor | union | find |
|---|---|---|---|
| quick-find | N | N | 1 |
| quick-union | N | tree height | tree height |
| weighted quick-union | N | lgN | lgN |
| weighted quick-union with path compression | N | very, very nearly, but not quite 1 | same as union |
| impossible | N | 1 | 1 |
Analysis of Algorithms
Scientific method
The very same approach that scientists use to understand the natural world is effective for studying the running time of programs.
- Observe some feature of the natural world, generally with precise measurement.
- Hypothesize a model that is consistent with observations.
- Predict events using the hypothesis.
- Verify the predictions by making further observations.
- Valitate by repeating until the hypothesis and observations agree.
Mathematical models
- Tilde approximations. We use tilde approximations, where we throw away low-order terms that complicate formulas. We write ~f(N) to represent any function that when divided by f(N) approaches 1 as N grows. We write g(N)~f(N) to indicate that g(N)/f(N) approaches 1 as N grows.
- Order-of-growth classifications. Most often, we work with tilde approximations of the form g(N)~af(N) where $ f(N) = N^b log_c N $ and refer to f(N) as the The order of growth of g(N). We use just a few structural primitives (statements, conditionals, loops, nesting, and method calls) to implement algorithms, so very often the order of growth of the cost is one of just a few functions of the problem size N.
| function | tilde approximation | order of growth |
|---|---|---|
| $ \frac{N^3}{6}-\frac{N^2}{2}+\frac N 3 $ | $~\frac{N^3}{6} $ | $N^3$ |
| $ \frac{N^3}{2}-\frac N 2$ | $ ~\frac{N^2}{2} $ | $N^2$ |
| $lgN+1 $ | $~lgN$ | $lgN$ |
| 3 | ~3 | 1 |
- Cost model. We focus attention on properties of algorithms by articulating a cost model that defines the basic operations. For example, an appropriate cost model for the 3-sum problem is the number of times we access an array entry, for read or write.
Commonly-used Notations in the Theory of Algorithms
| notation | provides | example | shorthand for | used to |
|---|---|---|---|---|
| Big Theta | asympatotic order of growth | $ \Theta (N^2) $ | $\frac 1 2 N^2, 5N^2+22NlogN+3N$ | classify algorithms |
| Big Oh | $\Theta (N^2)$and smaller | $O(N^2)$ | $10N^2,\ 100N, 22NlogN+3N $ | develop upper bounds |
| Big Omega | $\Theta (N^2)$and larger | $\Omega (N^2)$ | $\frac 1 2 N^2, N^5, N^3+22NlogN+3N $ | develop lower bounds |
1.4.6
Give the order of growth (as a function of N ) of the running times of each of the following code fragments:
int sum = 0;
for (int n = N; n > 0; n /= 2)
for(int i = 0; i < n; i++)
sum++;
$$ N+\frac N 2+\frac N 4+\frac N 8+…+1=2N-1\ \ \sim 2N $$ 所以是线性
int sum = 0;
for (int i = 1 i < N; i *= 2)
for (int j = 0; j < i; j++)
sum++;
$$ 1+2+4+8+…+2^{\lfloor lgN \rfloor}=2^{\lfloor lgN \rfloor + 1}-1\ \ \sim 2N$$ 所以是线性
int sum = 0;
for (int i = 1 i < N; i *= 2)
for (int j = 0; j < N; j++)
sum++;
$$ NlgN $$ 线性对数
1.4.15
Faster 3-sum. As a warmup, develop an implementation TwoSumFaster that uses a linear algorithm to count the pairs that sum to zero after the array is sorted (in stead of the binary-search-based linearithmic algorithm). Then apply a similar idea to develop a quadratic algorithm for the 3-sum problem.
public static int twoSumFaster(int[] a) {
int lo = 0, hi = a.length - 1;
int cnt = 0;
while (lo < hi) {
if (a[lo] + a[hi] == 0) {
cnt++;
lo++;
hi--;
} else if (a[lo] + a[hi] > 0)
hi--;
else
lo++;
}
return cnt;
}
public static int threeSumFaster(int[] a) {
int cnt = 0;
for (int i = 0; i < a.length; i++) {
int lo = i + 1, hi = a.length - 1;
while (lo < hi) {
if (a[i] + a[lo] + a[hi] == 0) {
cnt++;
lo++;
hi--;
} else if (a[i] + a[lo] + a[hi] > 0)
hi--;
else
lo++;
}
}
return cnt;
}
MegerSort
Implementation
public class Merge {
private static boolean isSorted(Comparable[] a, int lo, int hi) {
for (int i = lo + 1; i <= hi; i++)
if (less(a[i], a[i - 1])) return false;
return true;
}
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
assert isSorted(a, lo, mid);
assert isSorted(a, mid + 1, hi);
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
int i = lo, j = mid + 1;
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
assert isSorted(a, lo, hi);
}
private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
sort(aux, a, lo, mid);
sort(aux, a, mid+1, hi);
merge(a, aux, lo, mid, hi);
}
public static void sort(Comparable[] a) {
Comparable[] aux = new Comparable[a.length];
sort(a, aux, 0, a.length - 1);
}
public static void main(String[] args) {
int N = StdIn.readInt();
Comparable[] a = new Comparable[N];
for (int i = 0; i < N; i++)
a[i] = StdRandom.uniform(-10000,10000);
Stopwatch stopwatch = new Stopwatch();
sort(a);
for (var i : a) {
System.out.print(i + " ");
}
System.out.println();
System.out.println(stopwatch.elapsedTime());
}
}
Empirical analysis
The number of compares $C(N)$ and array accesses $A(N)$ to mergesort an array of size N satisfy the recurrences:
$$ C(N) \le C(\lceil{\frac N 2}\rceil) + C(\lfloor{\frac N 2}\rfloor) + N\ \ for N > 1,with \ C(1)=0. $$
$$
A(N) \le A(\lceil{\frac N 2}\rceil) + A(\lfloor{\frac N 2}\rfloor) + 6N\ \ for N > 1,with \ A(1)=0.
$$
we solve the recurrence when $ N $ is a power of 2.
$$ D(N) = 2D(\frac N 2) + N, for N > 1, with\ D(1) = 0. $$
Divide-and-conquer recurrence:
proof by picture

proof by expansion
$$ \begin{aligned} D(N)&=2D(N/2)+N \cr {D(N)} /{N} &= 2D(N / 2)/N + 1\cr &= D(N/2)/(N/2)+1 \cr &= D(N/4)/(N/4) + 1 + 1\cr &= D(N/8)/(N/8) + 1 + 1 + 1\cr …\cr &= D(N/N)/(N/N)+1+1+…+1\cr &= lgN \end{aligned} $$
proof by induction
- Base case: $N = 1$
- Induction hypothesis: $D(N)=Nlg(N)$.
- Goal: showthat $ D(2N) = (2N)lg(2N).$
$$ \begin{aligned} D(2N) &= 2D(N)+2N \cr &= 2NlgN+2N \cr &= 2N(lgN+1) \cr &= 2Nlg(2N) \end{aligned} $$
practical improvements
private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
// Use insertion sort for samll subarrays.
final int CUTOFF = 7;
if (hi <= lo + CUTOFF - 1) {
Insertion.sort(a, lo, hi);
return;
}
int mid = lo + (hi - lo) / 2;
sort(a, aux, lo, mid);
sort(a, aux, mid + 1, hi);
// Stop if already sorted.
if (!less(a[mid+1], a[mid])) return;
merge(a, aux, lo, mid, hi);
}
Eliminate the copy to the auxiliary array.
private static void merge(Comparable[] a,Comparable[] aux, int lo, int mid, int hi) {
int i = lo, j = mid + 1;
for (int k = lo; k <= hi; k++) {
if (i > mid) aux[k] = a[j++];
else if (j > hi) aux[k] = a[i++];
else if (less(a[j], a[i])) aux[k] =a[j++];
else aux[k] = a[i++];
}
}
private static void sort(Comparable[] a,Comparable[] aux, int lo, int hi) {
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
//switch soles of aux[] and a[]
sort(aux, a, lo, mid);
sort(aux, a, mid+1, hi);
merge(a, aux, lo, mid, hi);
}
Bottom-up mergesort
Implementation
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
int i = lo, j = mid + 1;
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k]= aux[j++];
else a[k] = aux[i++];
}
}
public static void sort(Comparable[] a) {
int N = a.length;
Comparable[] aux = new Comparable[N];
for (int sz = 1; sz < N; sz = sz + sz)
for (int lo = 0; lo < N - sz; lo +=sz + sz)
merge(a, aux, lo, lo + sz -1,Math.min(lo+sz+sz-1, N-1));
}
public static void main(String[] args) {
int N = StdIn.readInt();
Comparable[] a = new Comparable[N];
for (int i = 0; i < N; i++)
a[i] = StdRandom.uniform(-1000010000);
Stopwatch stopwatch = new Stopwatch();
sort(a);
for (var i : a) {
System.out.print(i + " ");
}
System.out.println();
System.out.println(stopwatch.elapsedTim());
}
Sorting Complexity
- Model of computation: decision tree.
- Cost model: # compares.
- Upper bound: $\sim NlgN $from mergesort
- Lower bound: ?
- Optimal algorithm: ?
Compare-based lower bound for sorting
Proposition. Any Compare-based sorting algorothm must use at least $lg(N!)\sim NlogN $(Stirling formula) compares in the worst-case.
Pf.
- Assume array consists of $N$ distinct values $a_1$ through $ a_n $.
- Worst case dictated by height $h$ of decision tree.
- Binary tree of height $h$ has at most $2^h$ leaves.
- $N! $different orderings $\Rightarrow$ at least $ N!$ leaves.
$$ \begin{aligned} 2^h \ge #leaves \ge N! \cr \Rightarrow h \ge lg(N!)\sim NlgN \end{aligned}$$
Stability
- Insertion sort is stable: Equal items never move fast each other.
private static void insertionSort(Comparable[] a) { int N = a.length; for (int i = 0; i < N; i++) { for (int j = i; j > 0 && less(a[j], a[j - 1]); j--) exch(a, j, j - 1); } } - Selection sort is not stable: Long-distance exchange might move an item past some equal item.
private static void selectionSort(Comparable[] a) { int N = a.length; for (int i = 0; i < N; i++) { int min = i; for (int j = i + 1; j < N; j++) if (less(a[j], a[min])) min = j; exch(a, i, min); } } - Shellsort is not stable: Long-distence exchange.
private static void shellSort(Comparable[] a) { int N = a.length; int h = 1; while (h < N / 3) h = 3 * h + 1; while (h >= 1) { for (int i = h; i < N; i++) { for (int j = i; j > h && less(a[j], a[j - h]); j -= h) exch(a, j, j - h); } h /= 3; } } - Mergesort is stable.: Suffices to verify that merge operation is table.
2.2.2
Give traces, in the style of the trace given with Algorithm 2.4, showing how the keys E A S Y Q U E S T I O N are sorted with top-down mergesort.
| a[] | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| lo | mid | hi | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| E | A | S | Y | Q | U | E | S | T | I | O | N | |||
| 0 | 0 | 1 | A | E | S | Y | Q | U | E | S | T | I | O | N |
| 0 | 1 | 2 | A | E | S | Y | Q | U | E | S | T | I | O | N |
| 3 | 3 | 4 | A | E | S | Q | Y | U | E | S | T | I | O | N |
| 3 | 4 | 5 | A | E | S | Q | U | Y | E | S | T | I | O | N |
| 0 | 2 | 5 | A | E | Q | S | U | Y | E | S | T | I | O | N |
| 6 | 6 | 7 | A | E | Q | S | U | Y | E | S | T | I | O | N |
| 6 | 7 | 8 | A | E | Q | S | U | Y | E | S | T | I | O | N |
| 9 | 9 | 10 | A | E | Q | S | U | Y | E | S | T | I | O | N |
| 9 | 10 | 11 | A | E | Q | S | U | Y | E | S | T | I | N | O |
| 6 | 8 | 11 | A | E | Q | S | U | Y | E | I | N | O | S | T |
| 0 | 5 | 11 | A | E | E | I | N | O | Q | S | S | T | U | Y |
| A | E | E | I | N | O | Q | S | S | T | U | Y |
2.2.3
Answer Exercise 2.2.2 for bottom-up mergesort.
| a[] | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| lo | mid | hi | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| E | A | S | Y | Q | U | E | S | T | I | O | N | |||
| 0 | 0 | 1 | A | E | S | Y | Q | U | E | S | T | I | O | N |
| 2 | 2 | 3 | A | E | S | Y | Q | U | E | S | T | I | O | N |
| 4 | 4 | 5 | A | E | S | Y | Q | U | E | S | T | I | O | N |
| 6 | 6 | 7 | A | E | S | Y | Q | U | E | S | T | I | O | N |
| 8 | 8 | 9 | A | E | S | Y | Q | U | E | S | I | T | O | N |
| 10 | 10 | 11 | A | E | S | Y | Q | U | E | S | I | T | N | O |
| 0 | 1 | 3 | A | E | S | Y | Q | U | E | S | I | T | N | O |
| 4 | 5 | 7 | A | E | S | Y | E | Q | S | U | I | T | N | O |
| 8 | 9 | 11 | A | E | S | Y | E | Q | S | U | I | N | O | T |
| 0 | 3 | 7 | A | E | E | Q | S | S | U | Y | I | N | O | T |
| 0 | 7 | 11 | A | E | E | I | N | O | Q | S | S | T | U | Y |
| A | E | E | I | N | O | Q | S | S | T | U | Y |
2.2.4
Does the abstract in-place merge produce proper output if and only if the two input subarrays are in sorted order? Prove your answer, or provide a counterexample.(是否当且仅当两个输入的数组都有序时原地归并的抽象方法才能得到正确的结果?证明你的结论,或者给出一个反例。)
- 是的,只有当两个输入数组都有序时采用原地归并才能得到正确的结果。
- 反例:数组1:[4, 2, 3],数组2:[1, 5, 8];
按归并算法归并后得到[1,4,2,3,5,8]; 可以看到归并后元素的相对位置不变,故得到错误的结果。
2.2.5
Give the sequence of subarray sizes in the merges performed by both the top-down and the bottom-up mergesort algorithms, for N = 39. (当输入数组的大小N=39时,给出自顶向下和自底向上的归并排序中各归并子数组的大小及顺序。)
自顶向下
2, 3, 2, 5, 2, 3, 2, 5, 10, 2, 3, 2, 5, 2, 3, 2, 5, 10, 20, 2, 3, 2, 5, 2, 3, 2, 5, 10, 2, 3, 2, 5, 2, 2, 4, 9, 19, 39
自底向上
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 8, 8, 8, 8, 7, 16, 16, 32, 39
QuickSort
quicksort
Basic plan:
- Shuffle the array
- Partition so that, for some j
- entry a[j] in place
- no larger entry to the left of j
- no smaller entry to the right of j
- Sort each piece recursively.
Java implementation
public class Quick {
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
private static void exch(Comparable[] a, int i, int j) {
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
private static int partition(Comparable[] a, int lo, int hi) {
int i = lo, j = hi + 1;
while (true) {
while (less(a[++i], a[lo]))
if (i == hi) break;
while (less(a[lo], a[--j]))
if (j == lo) break;
if (i >= j) break;
exch(a, i, j);
}
exch(a, lo, j);
return j;
}
private static void sort(Comparable[] a) {
StdRandom.shuffle(a);
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi) {
if (lo >= hi) return;
int j = partition(a, lo, hi);
sort(a, lo, j - 1);
sort(a, j + 1, hi);
}
}
average-case analysis
$C_N $ satisfies the recurrence $C_0 = C_1=0$ and for $ N\ge 2 $:
$$ C_N = (N + 1) + (\frac{C_0+C_{N-1}}{N})+ (\frac{C_1+C_{N-2}}{N})+ … +(\frac{C_{N-1}+C_{0{N}}}) $$
Multiply both sides by N and collect terms: $$ NC_N = N(N+1)+2(C_0+C_1+…+C_{N-1}) $$
Substract this from the same equation for $N - 1$: $$ NC_N-(N-1)C_{N-1}=2N+2C_{N-1} $$
Rearrage terms and devide by $N(N+1)$: $$ \frac{C_N}{N+1} = \frac{C_{N-1{N}}} + \frac{2}{N+1} $$
Repeatedly apply above equation: $$ \begin{aligned} \frac{C_N}{N+1} &= \frac{C_{N-1}}{N}+\frac{2}{N+1} \cr &= \frac{C_{N-2}}{N-1}+\frac{2}{N}+\frac{2}{N+1} \cr &= \frac{C_{N-3}}{N-2}+\frac{2}{N-1}+\frac{2}{N}+\frac{2}{N+1} \cr &= \frac 2 3 + \frac 2 4 + \frac 2 5 +…+\frac 2 {N+1} \end{aligned} $$
Approximate sum by an integral: $$ \begin{aligned} C_N &= 2(N+1)(\frac 1 3 + \frac 1 4 + \frac 1 5 +…+ \frac{1}{N+1}) \cr & \sim 2(N+1) \int_{3}^{N+1}{\frac{1}{x}dx} \end{aligned} $$
Finally, the desired result: $$ C_N \sim 2(N+1)lnN \sim 1.39NlgN $$
3-way quicksort
template <typename T>
void threeWayQuickSort(T a[], int lo, int hi) {
if (hi <= lo) return;
int lt = lo, gt = hi;
T v = a[lo];
int i = lo;
while (i <= gt) {
if (a[i] < v)
swap(a[lt++], a[i++]);
else if (a[i] > v)
swap(a[gt--], a[i]);
else
i++;
}
threeWayQuickSort(a, lo, lt - 1);
threeWayQuickSort(a, gt + 1, hi);
}
2.3.1
Show, in the style of the trace given with partition(), how that method patitions the array E A S Y Q U E S T I O N.
| i | j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 12 | E | A | S | Y | Q | U | E | S | T | I | O | N |
| 2 | 6 | E | A | S | Y | Q | U | E | S | T | I | O | N |
| 2 | 6 | E | A | E | Y | Q | U | S | S | T | I | O | N |
| 3 | 2 | E | A | E | Y | Q | U | S | S | T | I | O | N |
| 2 | E | A | E | Y | Q | U | S | S | T | I | O | N |
2.3.2
Show, in the style of the quicksort trace given in this section, how quicksort sorts the array E A S Y Q U E S T I O N (for the purposes of this exercise, ignore the initial shuffle).

2.3.3
What is the maximum number of times during the execution of Quick.sort() that the largest item can be exchanged, for an array of length N ? (对于长度为N的数组,在Quick.sort()执行时,其最大的元素最多会被交换多少次?)
在Quick.sort()中,一个元素被交换可分为两种情况:
- 该元素是枢轴,在partition最后一步和j交换
- 该元素在本次partition中不是枢轴,出现在了枢轴错的一侧,需要被交换到另一侧
- 如果该元素是枢轴,那么在交换后它的位置就固定下来了,之后不再涉及交换,因此要使交换次数最大,这个元素应该是在每次partition时都位于枢轴错误的一侧,因为是最大的元素,所以应该总是在枢轴的左侧。
- 为了使得partition的次数尽可能的多,需要使得每次移动的距离短,这里我们先考虑每次移动一位,如数组[5,9,1,6,7]:
- 枢轴为5,交换后变为[5,1,9,6,7]
- 枢轴交换,变为[1,5,9,6,7]
- 我们发现在下一次partition中最大元素9会成为枢轴,不再被交换
- 所以考虑每次移动两位,如数组[2,10,4,1,6,3,8,5,7,9]
- 枢轴为2,交换后[2,1,4,10,6,3,8,5,7,9]
- 枢轴交换,变为[1,2,4,10,6,3,8,5,7,9]
- 枢轴为4,交换后[1,2,4,3,6,10,8,5,7,9]
- 枢轴交换,变为[1,2,3,4,6,10,8,5,7,9]
- 枢轴为6,交换后[1,2,3,4,6,5,8,10,7,9]
- 枢轴交换,变为[1,2,3,4,5,6,8,10,7,9]
- 枢轴为8,交换后[1,2,3,4,5,6,8,7,10,9]
- 枢轴交换,变为[1,2,3,4,5,6,7,8,10,9]
- 枢轴为10,交换后[1,2,3,4,5,6,7,8,9,10]
- 在上面这个N=10的数组中,“10”这个最大的元素一共被交换了5次,所以我们可以认为对于N个元素的数组,在执行Quick.sort()时最大元素最多会被交换N/2次。
2.3.4
Suppose that the initial random shuffle is omitted. Give six arrays of ten elements for which Quick.sort() uses the worst-case number of compares.
如果始终选第一个元素作为枢轴的话,要使比较次数达到最坏情况的话,输入数组应为升序。比较次数达到$ N + N-1 + N-2 + N-3 +…+1 = \frac{N(N+1)}{2} \sim N^2/2 $ 例如:
- [1,2,3,4,5,6,7,8,9,10]
- [2,4,6,8,10,12,14,16,18,20]
- [-1,1,3,5,7,9,11,13,15,17]
- [10,20,30,40,50,60,70,80,90,100]
- [5,10,15,20,25,30,35,40,45,50]
- [0,2,3,4,6,7,8,9,10,12]
2.3.5
Give a code fragment that sorts an array that is known to consist of items having just two distinct keys.
static void sort(Comparable[] a) {
int lo = 0, hi = a.length - 1;
int i = 0;
while (i <= hi) {
int tmp = a[i].compareTo(a[lo]);
if (tmp < 0) exch(a, lo++, i++);
else if (tmp > 0) exch(a, i, hi--);
else i++;
}
}
Priority Queues
API

binary-heap
Java implementation
public class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq;
private int N = 0;
public MaxPQ(int maxN) {
pq = (Key[]) new Comparable[maxN + 1];
}
public boolean isEmpty() {
return N == 0;
}
public int size() {
return N;
}
public void insert(Key v) {
pq[++N] = v;
swim(N);
}
public Key delMax() {
Key max = pq[1];
exch(1, N--);
sink(1);
pq[N+1] = null;
return max;
}
private boolean less(int i, int j) {
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i, int j) {
Key tmp = pq[i];
pq[i] = pq[j];
pq[j] = tmp;
}
private void swim(int k) {
while (k > 1 && less(k / 2, k)) {
exch(k / 2, k);
k /= 2;
}
}
private void sink(int k) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(j, j + 1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
}
heapsort
Basic plan for in-place sort
- Create max-heap with all N keys.
- Repatedly remove the maximum key.
Java implementation
public class Heap {
public static void sort(Comparable[] a) {
int N = a.length;
for (int k = N / 2; k >= 1; k--)
sink(a, k, N);
while (N > 1) {
exch(a, 1, N);
sink(a, 1, --N);
}
}
private static boolean less(Comparable a[], int i, int j) {
return a[i - 1].compareTo(a[j - 1]) < 0;
}
private static void exch(Comparable a[], int i, int j) {
Comparable t = a[i - 1];
a[i - 1] = a[j - 1];
a[j - 1] = t;
}
private static void sink(Comparable[] a, int k, int N) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(a, j, j + 1)) j++;
if (!less(a, k, j)) break;
exch(a, k, j);
k = j;
}
}
}
mathematical analysis
Proposition. Heap construction uses $ \le 2N $ compares and exchanges.
Proposition. Heapsort uses $ \le 2NlgN $ compares and exchanges.
Significance. In-place sorting algorithm with $ NlgN $ worst-case.
- Mergesort: no, linear extra space.
- Quicksort: no, quadratic time in worst case.
- Heapsort: yes!
Bottom line. Heapsort is optimal for both time and space but:
- Inner loop longer than quicksort’s.
- Makes poor use of cache memory.
- Not stable.
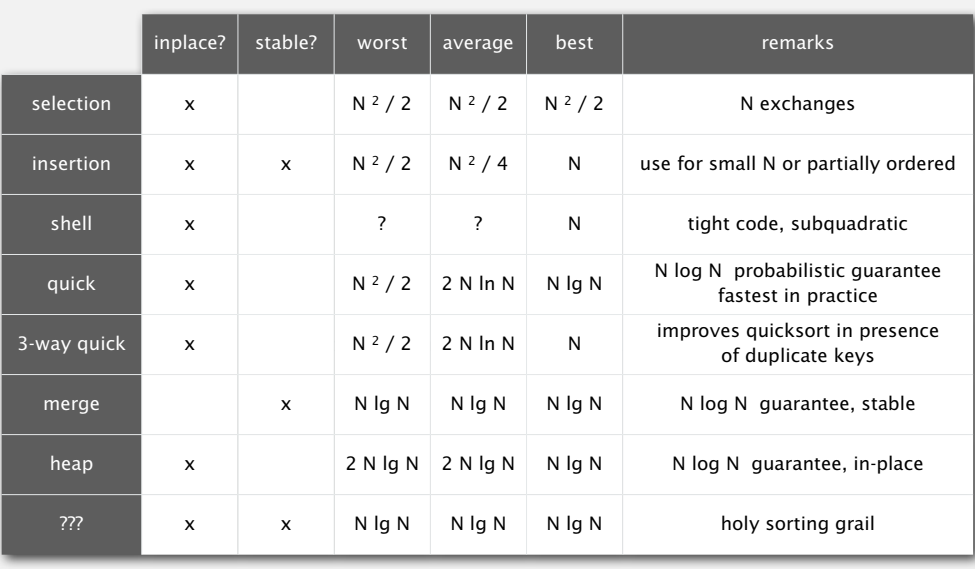
sorting-algorithms: summary
2.4.2
Criticize the following idea: To implement find the maximum in constant time, why not use a stack or a queue, but keep track of the maximum value inserted so far, then return that value for find the maximum?
如果用这种方法,当最大元素被删除之后,不能在常量时间内更新最大元素
2.4.3
Provide priority-queue implementations that support insert and remove the maximum, one for each of the following underlying data structures: unordered array, ordered array, unordered linked list, and linked list. Give a table of the worst-case bounds for each operation for each of your four implementations.
数组实现
public abstract class ArrayPQ<Key extends Comparable<Key>> {
protected Key[] pq;
protected int n;
public ArrayPQ(int capacity) {
pq = (Key[]) new Comparable[capacity];
n = 0;
}
public boolean isEmpty() {return n == 0;}
public int size() {return n;}
public abstract void insert(Key x);
public abstract Key delMax();
protected boolean less(int i, int j) {return pq[i].compareTo(pq[j]) < 0; }
protected void exch(int i, int j) {
Key t = pq[i];
pq[i] = pq[j];
pq[j] = t;
}
public static void main(String[] args) {
OrderedArrayMaxPQ pq = new OrderedArrayMaxPQ(10);
pq.insert("this");
pq.insert("is");
pq.insert("a");
pq.insert("test");
while (!pq.isEmpty())
System.out.println(pq.delMax());
}
}
class UnorderedArrayMaxPQ<Key extends Comparable<Key>> extends ArrayPQ<Key> {
public UnorderedArrayMaxPQ(int capacity) {
super(capacity);
}
@Override
public void insert(Key x) {
pq[n++] = x;
}
@Override
public Key delMax() {
int max = 0;
for (int i = 1; i < n; i++) {
if (less(max, i)) max = i;
exch(max, n-1);
}
return pq[--n];
}
}
class OrderedArrayMaxPQ<Key extends Comparable<Key>> extends ArrayPQ<Key>{
public OrderedArrayMaxPQ(int capacity) {
super(capacity);
}
@Override
public void insert(Key x) {
int i = n - 1;
while (i >= 0 && x.compareTo(pq[i]) < 0) {
pq[i+1] = pq[i];
i--;
}
pq[i+1] = x;
n++;
}
@Override
public Key delMax() {
return pq[--n];
}
}
链表实现
public abstract class LinkedListPQ<Key extends Comparable<Key>> {
protected LinkedList<Key> pq;
public LinkedListPQ() {
pq = new LinkedList<Key>();
}
public boolean isEmpty() {
return pq.size() == 0;
}
public int size() {
return pq.size();
}
public abstract void insert(Key x);
public abstract Key delMax();
protected boolean less(Key a, Key b) {
return a.compareTo(b) < 0;
}
public static void main(String[] args) {
UnorderedLinkedMaxPQ pq = new UnorderedLinkedMaxPQ();
pq.insert("this");
pq.insert("is");
pq.insert("a");
pq.insert("test");
while (!pq.isEmpty())
System.out.println(pq.delMax());
}
}
class UnorderedLinkedMaxPQ<Key extends Comparable<Key>> extends LinkedListPQ<Key> {
@Override
public void insert(Key x) {
pq.addLast(x);
}
@Override
public Key delMax() {
int i = 0;
int idx = 0;
var max = pq.getFirst();
for (var e : pq) {
if (less(max, e)) {
max = e;
idx = i;
}
i++;
}
pq.remove(idx);
return max;
}
}
class OrderedLinkedMaxPQ<Key extends Comparable<Key>> extends LinkedListPQ<Key> {
public OrderedLinkedMaxPQ() {
super();
}
@Override
public void insert(Key x) {
int i = 0;
Iterator it = pq.iterator();
while (it.hasNext()) {
if (less(x, (Key) it.next())) break;
i++;
}
pq.add(i, x);
System.out.println(i + " eee ");
}
@Override
public Key delMax() {
return pq.removeLast();
}
}
the worst-case bounds
| insert() | delMax() | |
|---|---|---|
| 无序数组 | 1 | N |
| 有序数组 | N | 1 |
| 无序链表 | 1 | N |
| 有序链表 | N | 1 |
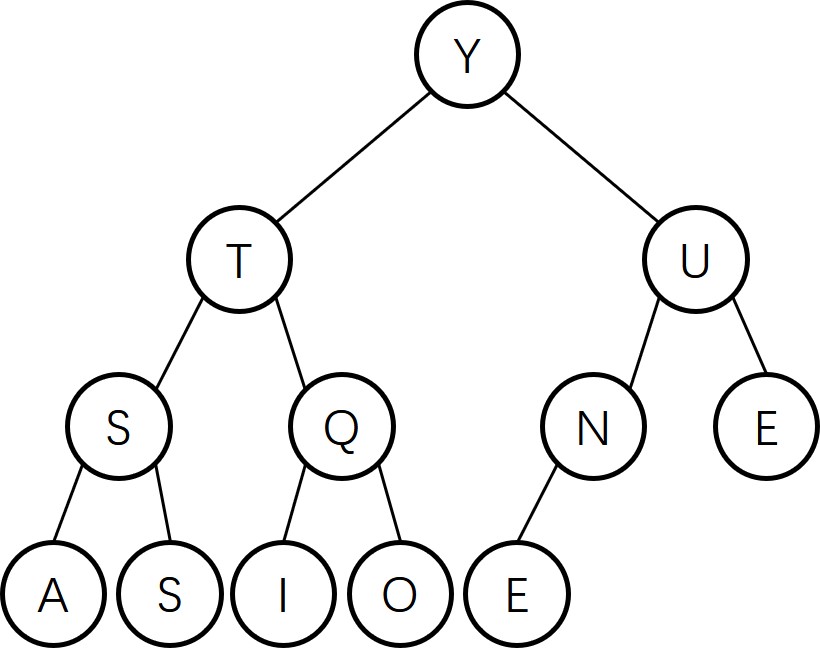
2.4.5
Give the heap that results when the keys E A S Y Q U E S T I O N are inserted in that order into an initially empty max-oriented heap.
2.4.7
The largest item in a heap must appear in position 1, and the second largest must be in position 2 or position 3. Give the list of positions in a heap of size 31 where the kth largest (i) can appear, and (ii) cannot appear, for k=2, 3, 4 (assuming the values to be distinct).
- k = 2:可能出现在2,3;不可能出现在1, 4~31
- k = 3:可能出现在2,3,4,5,6,7;不可能出现在1,8~31
- k = 4:可能出现在2,3,4,5,6,7,8,9,10,11,12,13,14,15,不可能出现在1,16~31
第k大元素只可能出现在深度不大于k的位置($ position \le 2^k-1 ,k \ge 2$)
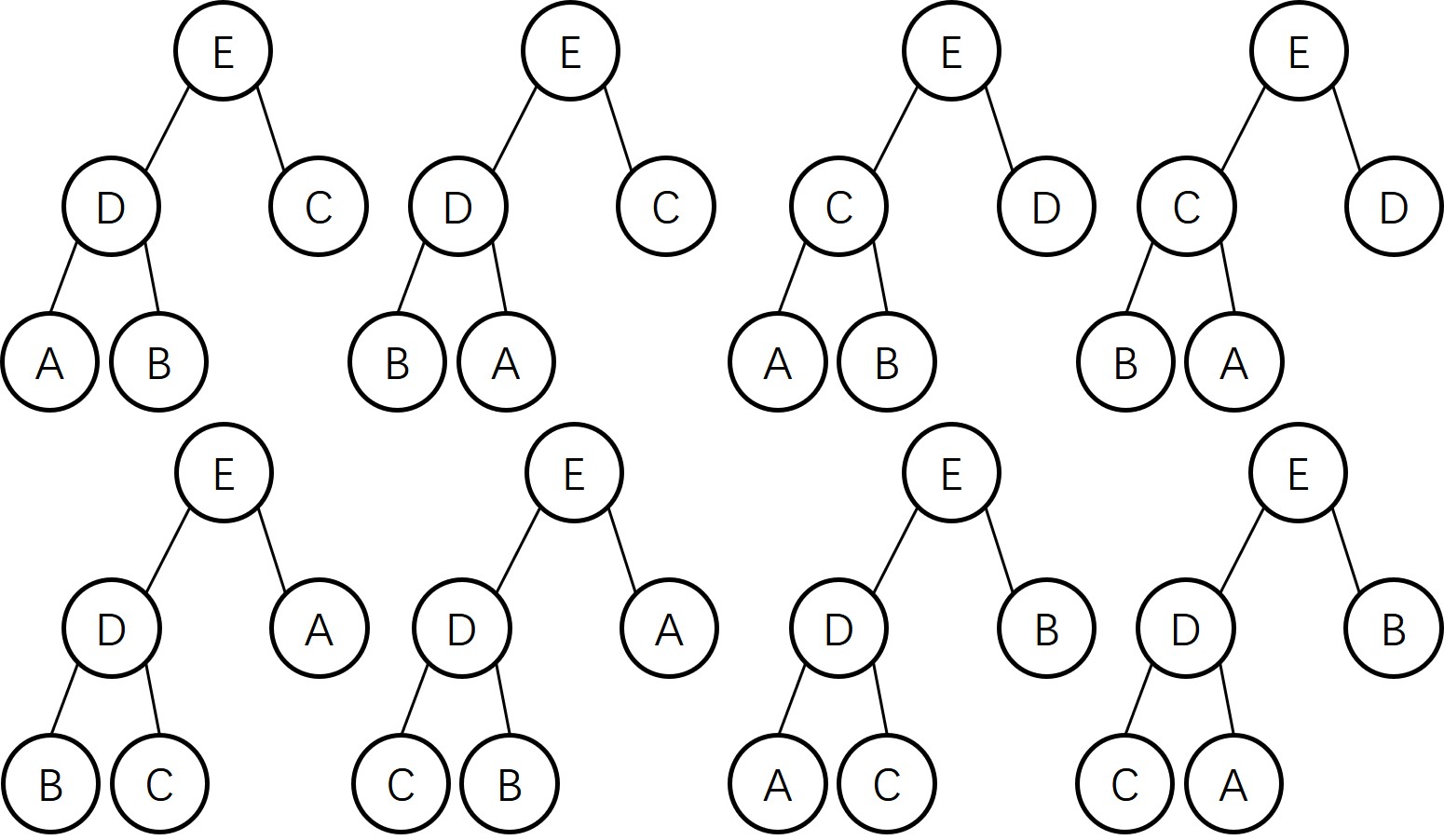
2.4.9
Draw all of the different heaps that can be made from the five keys A B C D E, then draw all of the different heaps that can be made from the five keys A A A B B.
A B C D E
- 最大堆
- 最小堆
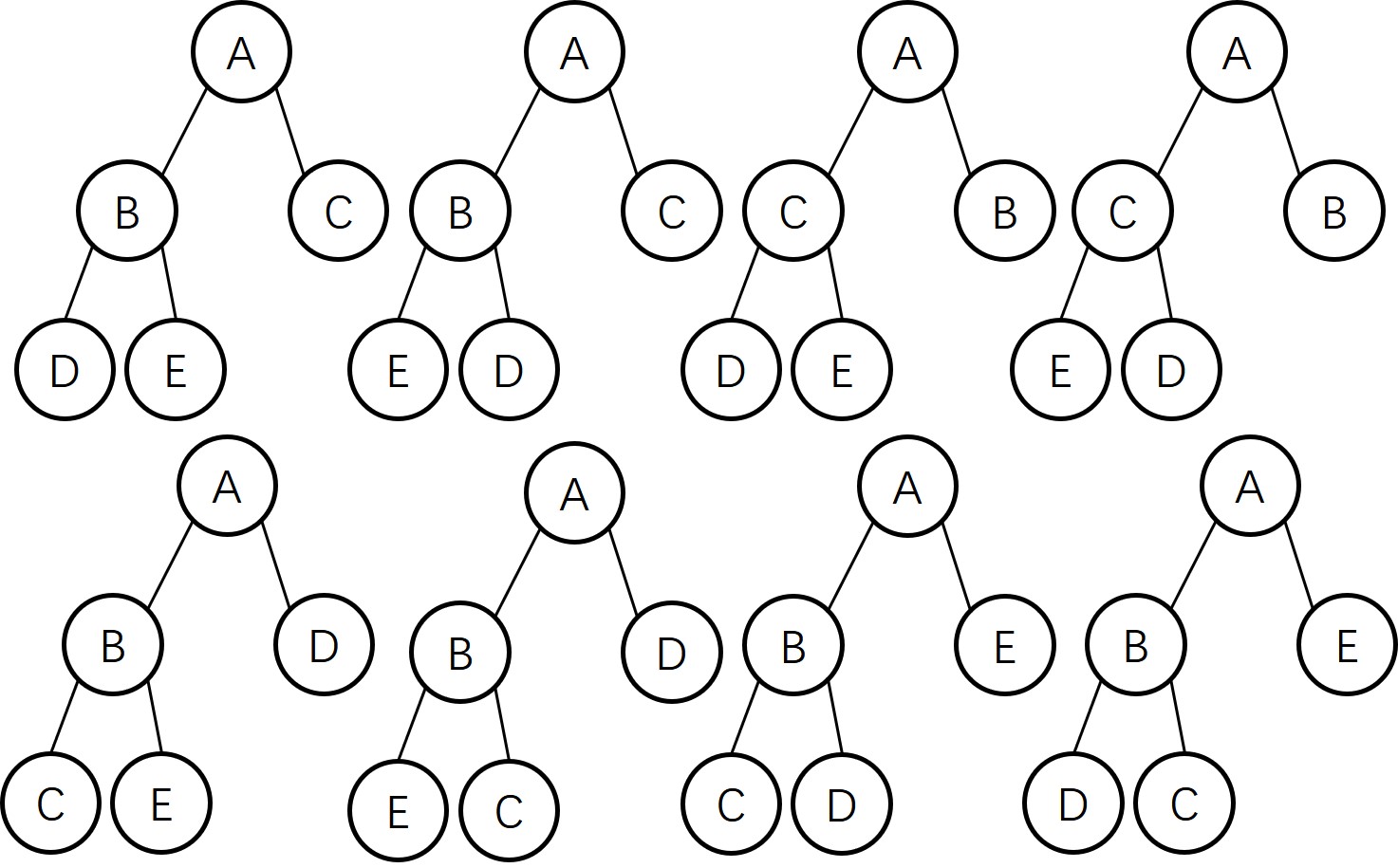
A A A B B
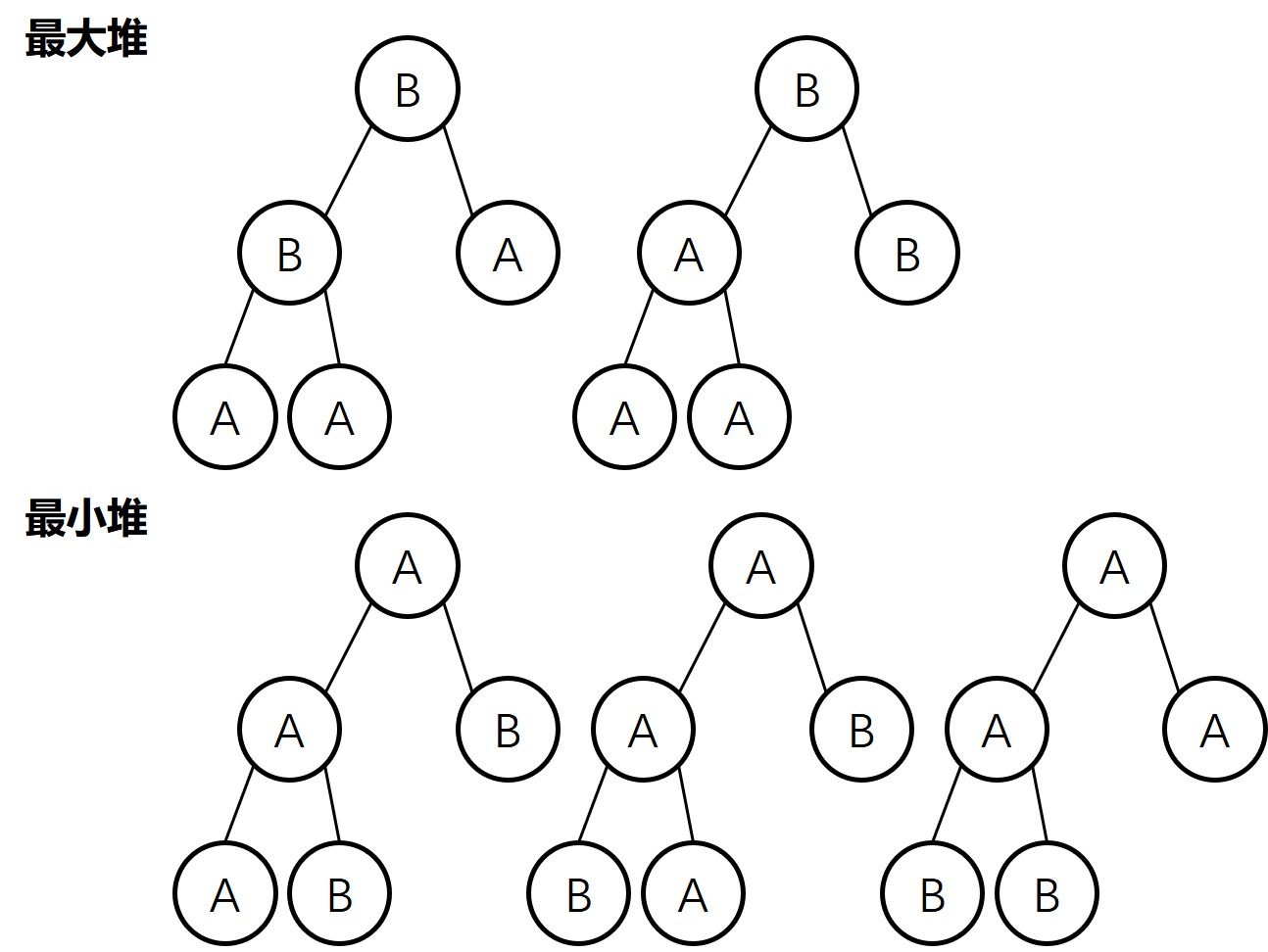
2.4.11
Suppose that your application will have a huge number of insert operations, but only a few remove the maximum operations. Which priority-queue implementation do you think would be most effective: heap, unordered array, or ordered array?
因为有大量的insert操作和很少的delMax操作,而heap, unordered array, ordered array实现的Priority Queue insert操作的花费时间的数量级分别为lgN, 1, N, 所以unordered array是最有效的。
2.4.12
Suppose that your application will have a huge number of find the maximum operations, but a relatively small number of insert and remove the maximum operations. Which priority-queue implementation do you think would be most effective: heap, unordered array, or ordered array?
大量的查找最大元素,heap和ordered array查找最大元素都是常量时间,但heap插入和删除最大元素都是lgN,而ordered array插入和删除分别是N和常量时间,综合下来,heap是最有效的。
UNDIRECTED GRAPHS
depth-first-search
public class DepthFirstPaths {
private boolean[] marked;
private int[] edgeTo;
private int s;
public DepthFirstPaths(Graph G,int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
Arrays.fill(marked, false);
this.s = s;
dfs(G, s);
}
private void dfs(Graph G, int v) {
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) {
dfs(G, w);
edgeTo[w] = v;
}
}
}
public boolean hasPathTo(int v) {
return marked[v];
}
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v)) return null;
Stack<Integer> path = new Stack<>();
for (int x = v; x != s; x = edgeTo[x])
path.push(x);
path.push(s);
return path;
}
public static void main(String[] args) {
int V = StdIn.readInt();
Graph g = new Graph(V);
int E = StdIn.readInt();
for (int i = 0; i < E; i++) {
g.addEdge(StdIn.readInt(), StdIn.readInt());
}
DepthFirstPaths dfp = new DepthFirstPaths(g, 0);
for (var i : dfp.pathTo(3)) {
System.out.println(i);
}
}
}
breadth-first-search
public class BreadthFirstPaths {
private boolean[] marked;
private int[] edgeTo;
private int s;
public BreadthFirstPaths(Graph G, int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
bfs(G, s);
}
private void bfs(Graph G, int s) {
Queue<Integer> Q = new Queue<>();
Q.enqueue(s);
marked[s] = true;
while (!Q.isEmpty()) {
int v = Q.dequeue();
for (int w : G.adj(v)) {
if (!marked[w]) {
Q.enqueue(w);
marked[w] = true;
edgeTo[w] = v;
}
}
}
}
public boolean hasPathTo(int v) {
return marked[v];
}
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v)) return null;
Stack<Integer> path = new Stack<>();
for (int i = v; i != s; i = edgeTo[i])
path.push(i);
path.push(s);
return path;
}
public static void main(String[] args) {
int V = StdIn.readInt();
Graph g = new Graph(V);
int E = StdIn.readInt();
for (int i = 0; i < E; i++) {
g.addEdge(StdIn.readInt(), StdIn.readInt());
}
BreadthFirstPaths bfp = new BreadthFirstPaths(g, 0);
for (var i : bfp.pathTo(3)) {
System.out.println(i);
}
}
}
connected components
public class CC {
private boolean[] marked;
private int[] id;
private int count;
public CC(Graph G) {
marked = new boolean[G.V()];
id = new int[G.V()];
for (int v = 0; v < G.V(); v++) {
if (!marked[v]) {
dfs(G, v);
count++;
}
}
}
public int count() { return count; }
public int id(int v) { return id[v]; }
private void dfs(Graph G, int v) {
marked[v] = true;
id[v] = count;
for (int w : G.adj(v)) {
if (!marked[w])
dfs(G, w);
}
}
public static void main(String[] args) {
Graph G = new Graph(StdIn.readInt());
int E = StdIn.readInt();
for (int i = 0; i < E; i++)
G.addEdge(StdIn.readInt(), StdIn.readInt());
CC cc = new CC(G);
System.out.println(cc.count);
}
}
Minimum Spanning Trees
Greedy algorithm
Cut property
Def: A cut in a graph is a partition of its vertices into two(nonempty) sets.
Def: A Crossing edge connects a vertex in one set with a vertex in the other.
Cut property. Give any cut, the crossing edge of min weight is in the MST
- Pf. Suppose the min-weight crossing edge e is not in the MST
- Adding e to the MST creates a cycle
- Some other edge f in cycle must be a crossing edge
- Removing f and adding e is also a spanning tree
- Since weight of e is less than the weight of f,that spanning tree is lower weight
- Contradiction
- Pf. Suppose the min-weight crossing edge e is not in the MST
Kruskal’s algorithm
Consider edges in ascending order of weight.
- Add next edge to tree T unless so doing would create a cycle.
public class KruskalMST {
private Queue<Edge> mst = new Queue<>();
private double weight;
public KruskalMST(EdgeWeightedGraph G) {
weight = 0;
MinPQ<Edge> pq = new MinPQ<>();
for (var e : G.edges()) {
pq.insert(e);
}
UF uf = new UF(G.V());
while (!pq.isEmpty() && mst.size() < G.V() - 1) {
Edge e = pq.delMin();
int v = e.either(), w = e.other(v);
if (!uf.connected(v, w)) {
uf.union(v, w);
mst.enqueue(e);
weight += e.weight();
}
}
}
public Iterable<Edge> edges() {
return mst;
}
public double weight() {
return weight;
}
}
Prim’s algorithm
- Start with vertex 0 and greedy grow tree T
- Add to T the min weight with exactly one endpoint in T
- Repeat until V-1 edges
LazyPrim Implementation
public class LazyPrimMST {
private boolean[] marked;
private Queue<Edge> mst;
private MinPQ<Edge> pq;
public LazyPrimMST(EdgeWeightedGraph G) {
pq = new MinPQ<>();
mst = new Queue<>();
marked = new boolean[G.V()];
visit(G, 0);
while (!pq.isEmpty() && mst.size() < G.V() - 1) {
Edge e = pq.delMin();
int v = e.either(), w = e.other(v);
if (marked[v] && marked[w]) continue;
mst.enqueue(e);
if (!marked[v]) visit(G, v);
if (!marked[w]) visit(G, w);
}
}
private void visit(EdgeWeightedGraph G, int v) {
marked[v] = true;
for (Edge e : G.adj(v)) {
if (!marked[e.other(v)]) {
pq.insert(e);
}
}
}
public Iterable<Edge> mst() {
return mst;
}
}
Indexed priority queue implementation
- Start as same code as MinPQ
- Maintain parallel arrays keys[], pq[], and qp[] so that:
- keys[i] is the priority of i
- pq[i] is the index of the key in heap position i
- qp[i] is the heap position of the key with index i
- Use swim(qp[i]) implement decreaseKey(i, key).
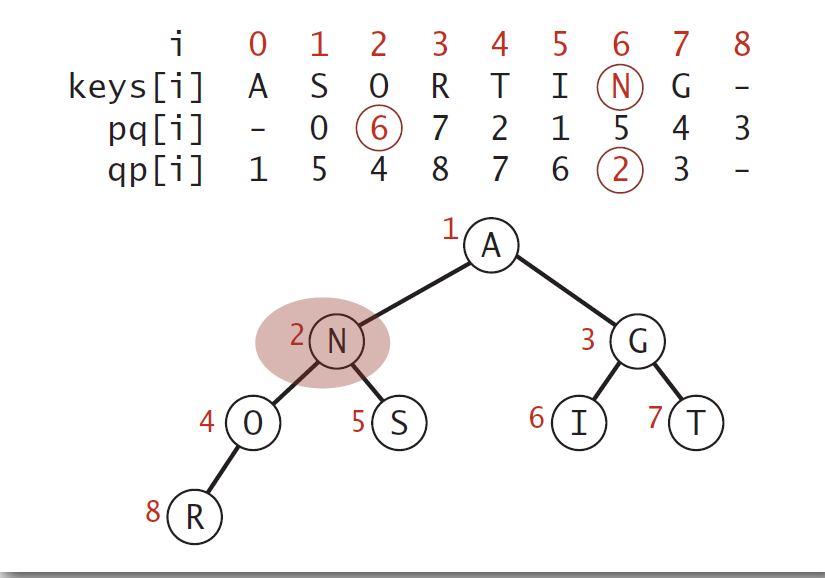
EagerPrim Implementation
import edu.princeton.cs.algs4.*;
public class PrimMST {
private Edge[] edgeTo;
private double[] distTo;
private boolean[] marked;
private IndexMinPQ<Double> pq;
public PrimMST(EdgeWeightedGraph G) {
edgeTo = new Edge[G.V()];
distTo = new double[G.V()];
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
pq = new IndexMinPQ<>(G.V());
distTo[0] = 0.0;
pq.insert(0, 0.0);
while (!pq.isEmpty())
visit(G, pq.delMin());
}
private void visit(EdgeWeightedGraph G, int v) {
marked[v] = true;
for (Edge e : G.adj(v)) {
int w = e.other(v);
if (marked[w]) continue;
if (e.weight() < distTo[w]) {
edgeTo[w] = e;
distTo[w] = e.weight();
if (pq.contains(w)) pq.change(w, distTo[w]);
else pq.insert(w, distTo[w]);
}
}
}
public Iterable<Edge> edges() {
Queue<Edge> mst = new Queue<>();
for (int v = 0; v < edgeTo.length; v++) {
Edge e = edgeTo[v];
if (e != null) {
mst.enqueue(e);
}
}
return mst;
}
public double weight() {
double weight = 0.0;
for (Edge e : edges()) {
weight += e.weight();
}
return weight;
}
}
4.3.2
Draw all of the MSTs of graph depicted at right (all edge weights are equal).
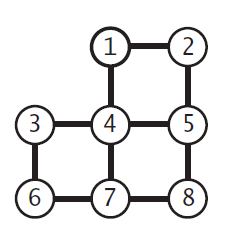
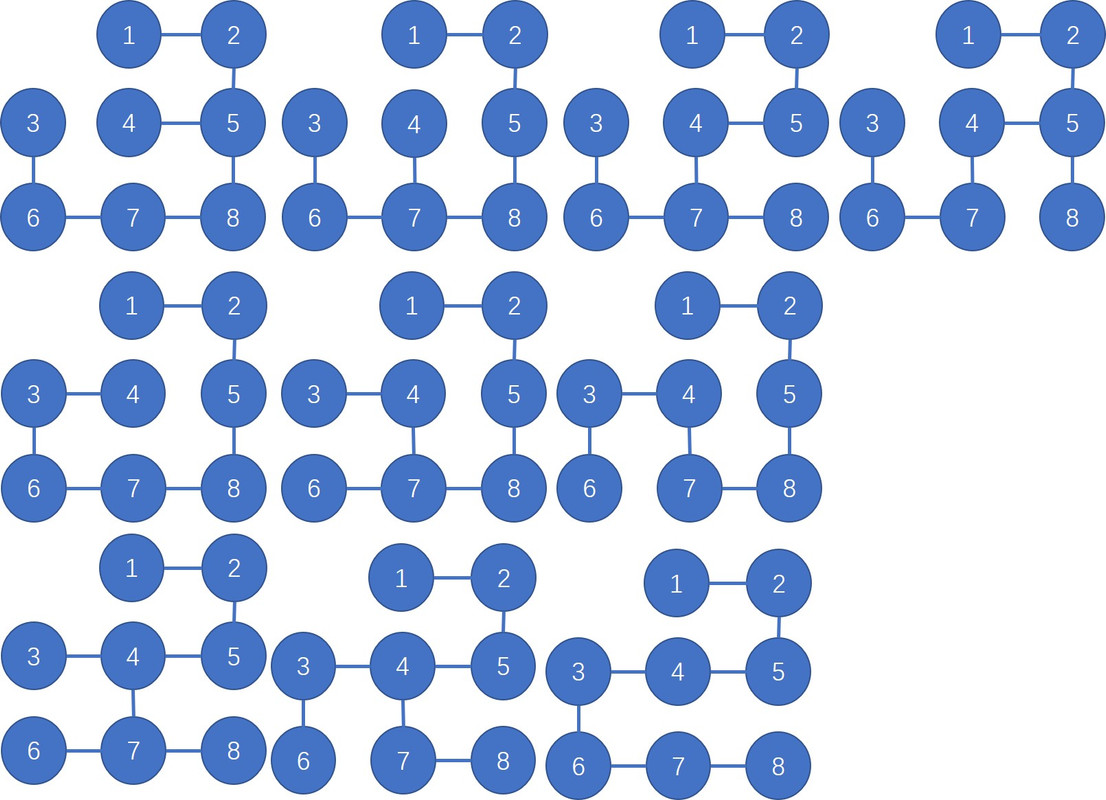
4.3.3
Show that if a graph’s edges all have distinct weights, the MST is unique
- 假设无向图G有两棵不同的最小生成树T1和T2
- e是在T1或T2中(但不是同时在两棵树中)最小权值的边,不妨假设e在T1中
- 将e添加到T2中会创建一个环C
- 在C中至少存在一条边f(但不在T1中,否则会产生环)
- 因为e是在T1或T2中(但不是同时在两棵树中)最小权值的边,并且每条边权值都不同
- 所以有e.weight < f.weight
- 用e代替f,将会产生比原来T2权值更小的生成树,产生了矛盾
4.3.13
Give a counterexample that shows why the following strategy does not necessarily find the MST: ‘Start with any vertex as a single-vertex MST, then add V-1 edges to it, always taking next a min-weight edge incident to the vertex most recently added to the MST.’
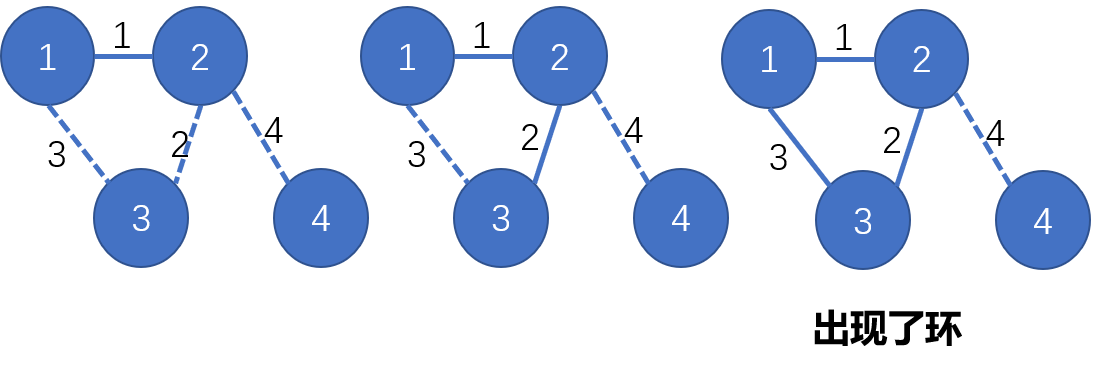
Shortest Paths
shortest-paths properties
Data structures for single-source shortest paths
- Goal. Find the shortest-paths from s to every other vertex.
- Observation. A shortest-paths tree (SPT) solution exists. Why?
- Consequence. Can represent the SPT with two vertex-indexed arrays:
- distTo[v] is length of shortest path from s to v
- edgeTo[v] is last edge on shortest path from s to v
Edge relaxation
- Relax edge e = v->w
- distTo[v] is length of shortest known path from s to v
- distTo[w] is length of shortest known path from s to w
- edgeTo[w] is last edge on shortest known path from s to w
- if e = v->w gives shorter path to w through v, update both distTo[w] and edgeTo[w]
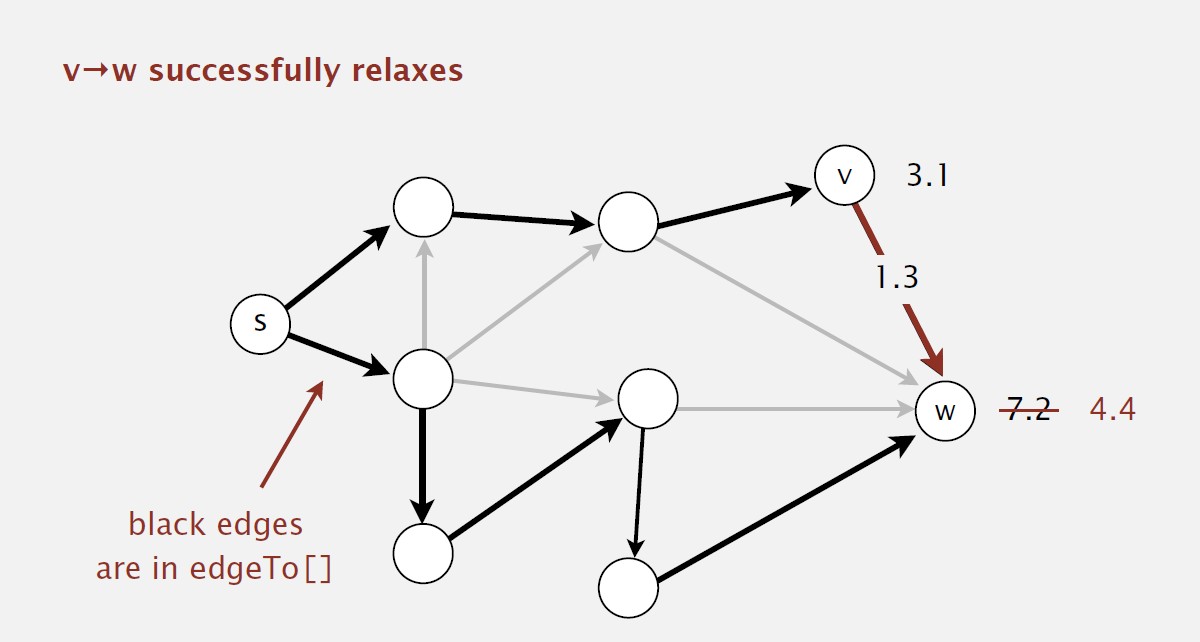
Shortest-paths optimality conditions
- Proposition. Let G be an edge-weighted digraph. Then distTo[] are the shortest path distances from s iff:
- distTo[s] = 0
- For each vertex v, distTo[v] is the length of some path from s to v
- For each edge e = v->w, distTo[w] <= distTo[v] + e.weight().
- Pf.
- suppose that distTo[w] > distTo[v] + e.weight() for some edge e = v->w.
- Then, e gives a path from s to w (through v) of length less than distTo[w].
- distTo[v1] <= distTo[v0] + e1.weight()
- distTo[v2] <= distTo[v1] + e2.weight()
- …
- distTo[vk] <= distTo[v(k-1)] + ek.weight()
- Add inequalities; simplify; and substitude distTo[v0] = distTo[s] = 0: distTo[w] = distTo[vk] <= e1.weight() + e2.weight() + … + ek.weight()
- Thus, distTo[w] is the weight of shortest path to w
Genertic shortest-paths algorithm
- Proposition. Genertic algorithm computes SPT(if it exists) from s.
- Pf sketch
- Throughout algorithm, distTo[v] is the length of a simple path from s to v (and edgeTo[v] is last edge on path)
- Each successful relaxation decreases distTo[v] from some v
- The entry distTo[v] can decrease at most a finite number of times
- Efficient implementataions How to choose which edge to relax?
- Ex 1. Dijkstra’s algorithm (nonnegative weights)
- Ex 2. Topological sort algorithm (no directed cycles)
- Ex 3. Bellman-Ford algorithm (no negative cycles)
Dijkstra’s algorithm
Dijkstra’s algorithm Demo
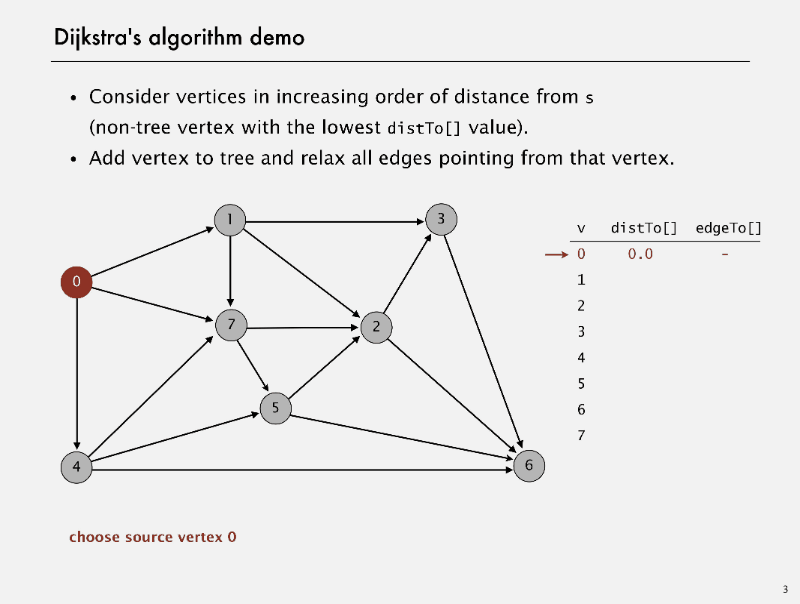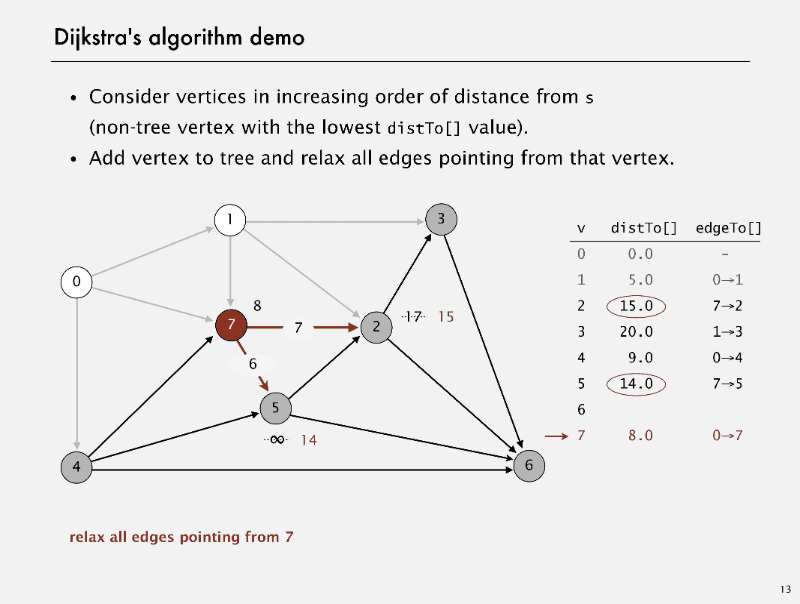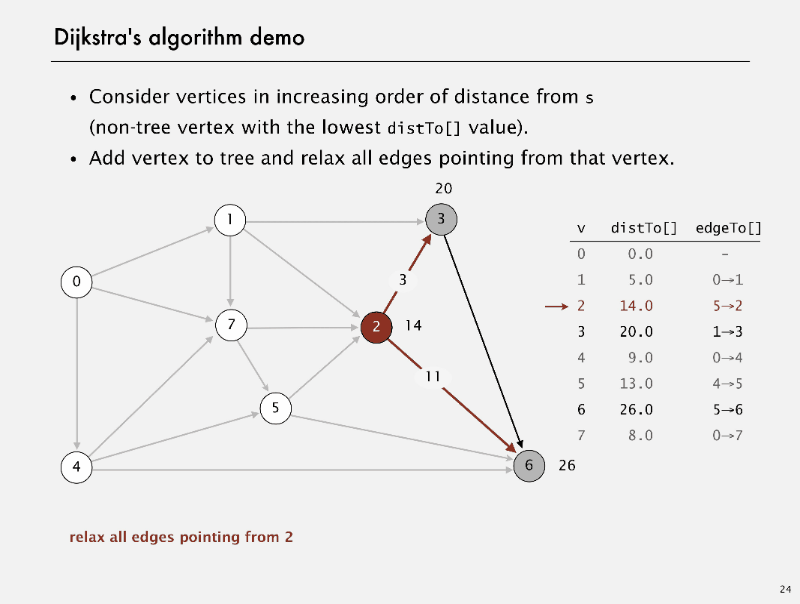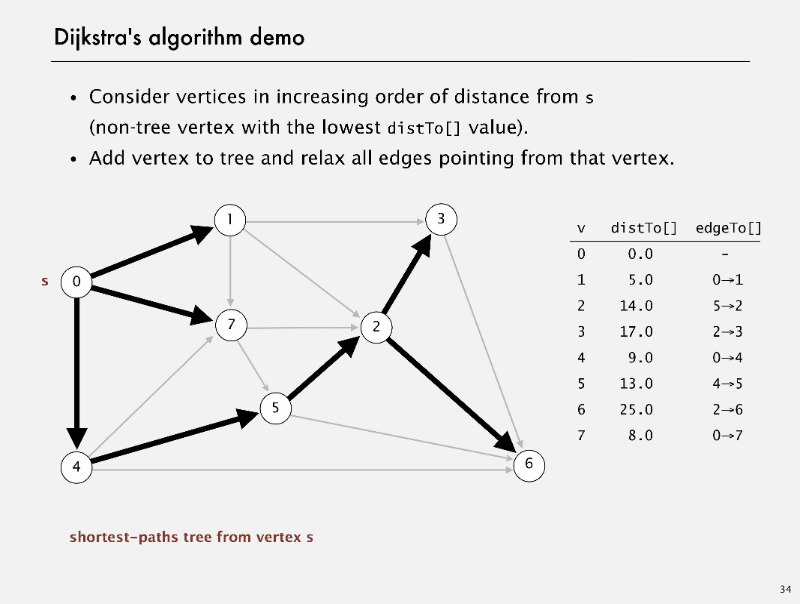
correctness proof
Proposition. Dijkstra’s algorithm computes a SPT in any edge-weighted diagraph with nonnegative weights.
Pf.
- Each edge e = v->w is relaxed exactly once (when v is relaxed), leaving distTo[w] <= distTo[v] + e.weight()
- Inequality hold until algorithm terminates because:
- distTo[w] cannot increase <- distTo[] values are monotone decreasing
- distTo[v] will not change <- we choose lowest distTo[] value at each step (and edge weights are nonnegative)
- Thus, opun termination, shortest-paths optimality conditions hold
Java implementation
public class DijkstraSP {
private DirectedEdge[] edgeTo;
private double[] distTo;
private IndexMinPQ<Double> pq;
public DijkstraSP(EdgeWeightedDigraph G, int s) {
edgeTo = new DirectedEdge[G.V()];
distTo = new double[G.V()];
pq = new IndexMinPQ<Double>(G.V());
for (int v = 0; v < G.V(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
distTo[s] = 0.0;
pq.insert(s, 0.0);
while (!pq.isEmpty()) {
int v = pq.delMin();
for (DirectedEdge e : G.adj(v))
relax(e);
}
}
private void relax(DirectedEdge e) {
int v = e.from(), w = e.to();
if (distTo[w] > distTo[v] + e.weight()) {
distTo[w] = distTo[v] + e.weight();
edgeTo[w] = e;
if (pq.contains(w)) pq.decreaseKey(w, distTo[w]);
else pq.insert(w, distTo[w]);
}
}
public double distTo(int v) { return distTo[v]; }
public Iterable<DirectedEdge> pathTo(int v) {
Stack<DirectedEdge> path = new Stack<>();
for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()])
path.push(e);
return path;
}
}
edge-weighted DAGs
Acyclic shortest paths demo
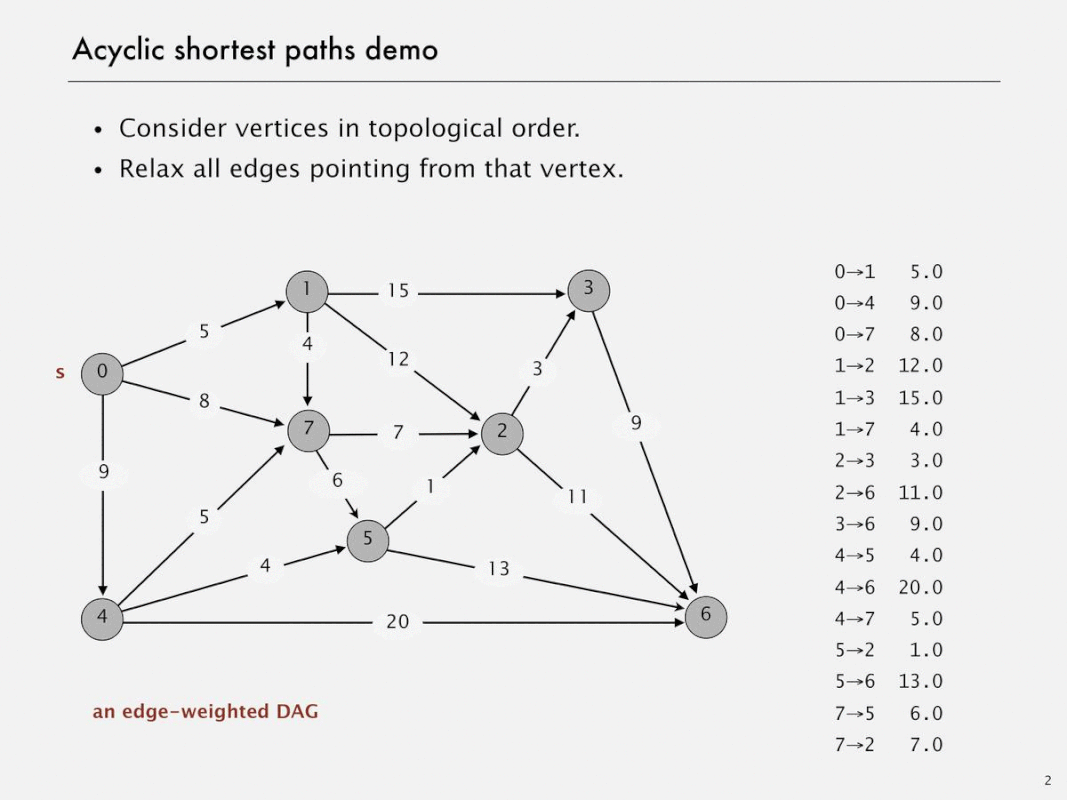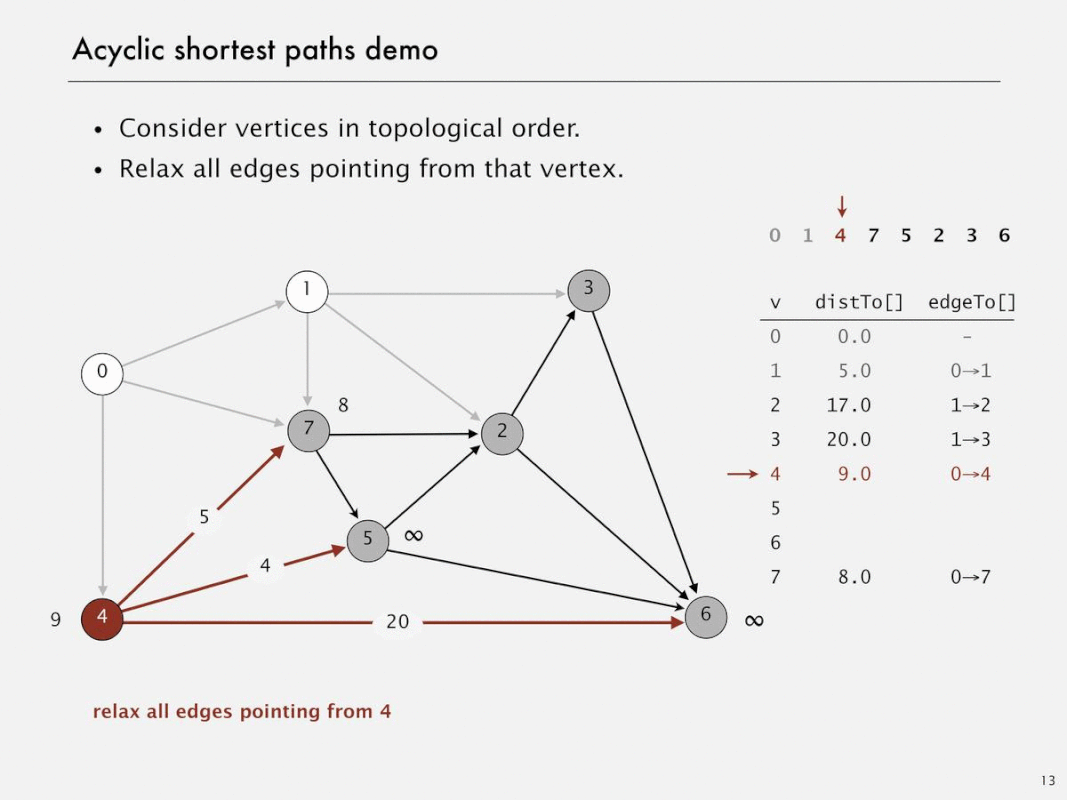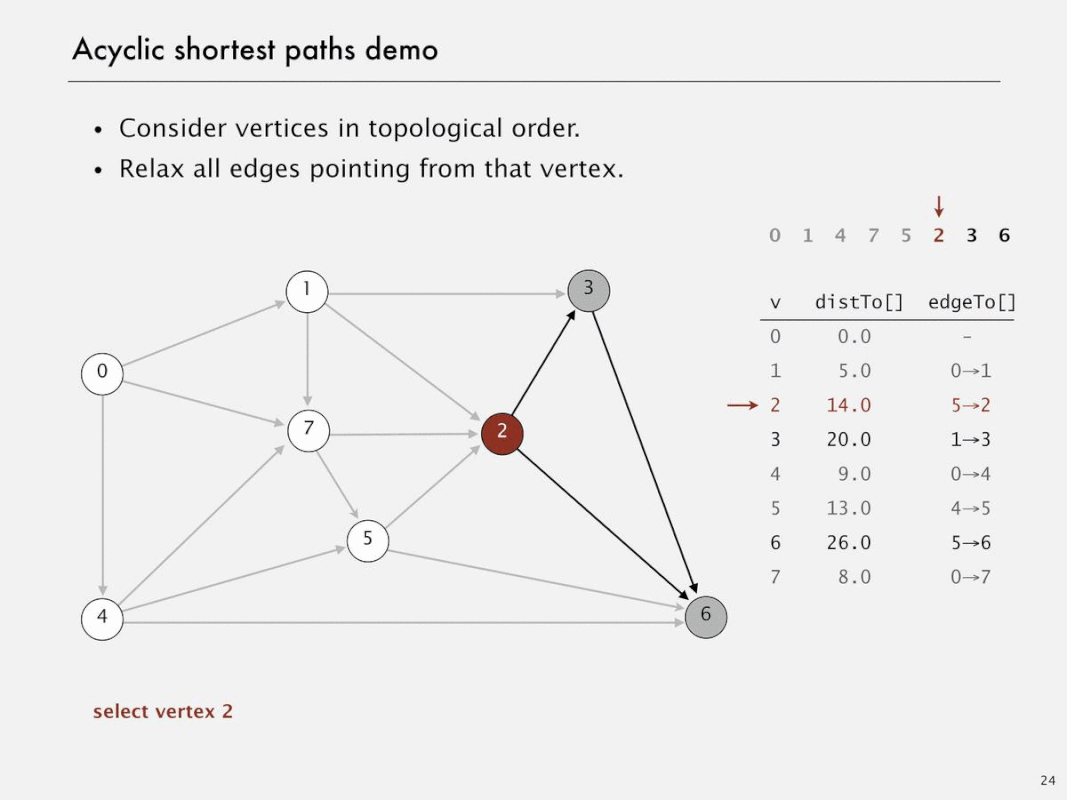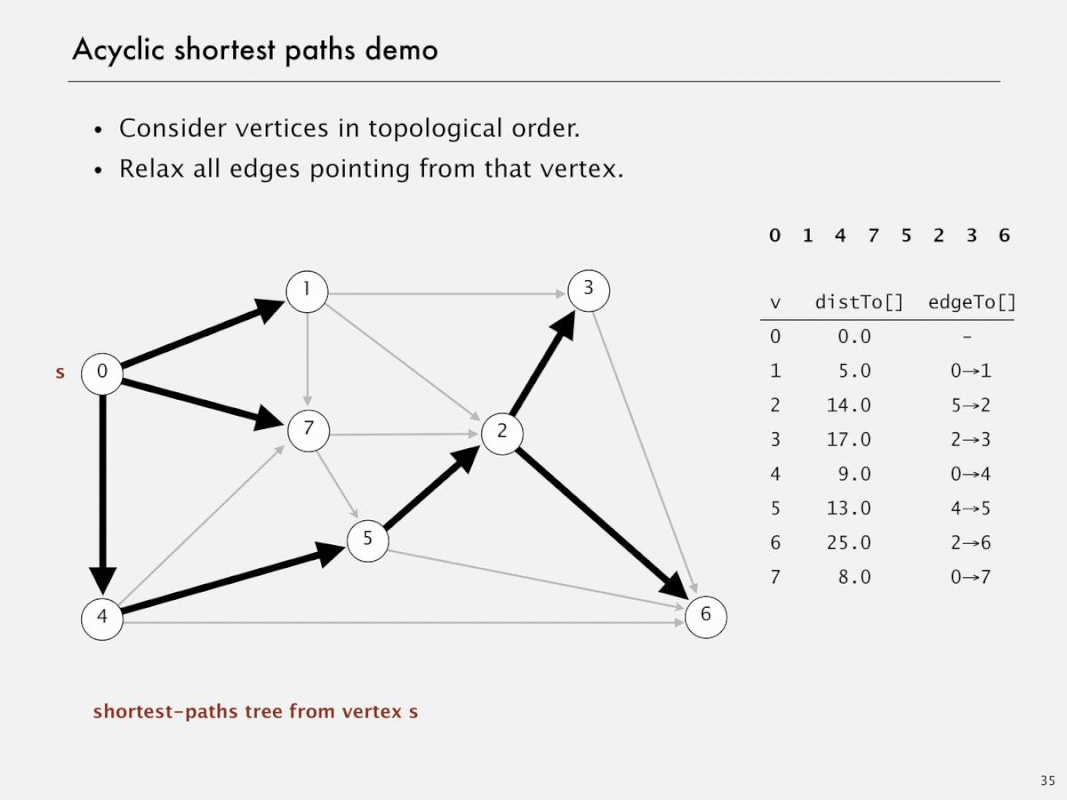
Shortest paths in edge-weighted DAGs
- Proposition. Topological sort algorithm computes SPT in any (edge weights can be negative!) edge-weighted DAG in time proportional to E + V
- Pf.
- Each edge e = v->w is relaxed exactly once (when v is relaxed), leaving distTo[w] <= distTo[v] + e.weight()
- Inequality holds until algorithm terminates because:
- distTo[w] cannot increase <- distTo[] values are monotone decreasing
- distTo[v] will not change <- because of topological order, no edge pointing to v will be relaxed after v is relaxed
- Thus, upon termination, shortest-paths optimality conditions hold
Java Implementation
public class AcyclicSP {
private DirectedEdge[] edgeTo;
private double[] distTo;
public AcyclicSP(EdgeWeightedDigraph G, int s) {
edgeTo = new DirectedEdge[G.V()];
distTo = new double[G.V()];
for (int v = 0; v < G.V(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
distTo[s] = 0.0;
Topological topological = new Topological(G);
for (int v : topological.order())
for (DirectedEdge e : G.adj(v))
relax(e);
}
private void relax(DirectedEdge e) {
int v = e.from(), w = e.to();
if (distTo[w] > distTo[v] + e.weight()) {
distTo[w] = distTo[v] + e.weight();
edgeTo[w] = e;
}
}
public Iterable<DirectedEdge> pathTo(int v) {
Stack<DirectedEdge> path = new Stack<>();
for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()])
path.push(e);
return path;
}
}
negative weights
- Def. A negative cycle is a directed cycle whose sum of edge weights is negative.
- Proposition. A SPT exists iff no negative cycles.
Bellman-Ford algorithm: analysis
Initialize distTo[s] = 0 and distTo[v] = $ \infty $ for all other vertices.
Repeat V times:
- Relax each edge.
Proposition. Dynamic programming algorithm computes SPT in any edge-weighted digraph with no negative cycles in time proportional to $E\times V$
Pf idea. After pass i, found shortest path containing at most i edges.
Bellman-Ford algorithm: practical improvement
Observation. If distTo[v] does not change during pass i, no need to relax any edge pointing from v in pass i+1.
FIFO implementation. Maintain queue of vertices whose distTo[] changed.
Overall effect.
- The running time is still proportional to $E \times V $ in worst case.
- But much faster than that in practice.
Bellman-Ford Java implementation
public class BellmanFordSP {
private double[] distTo;
private DirectedEdge[] edgeTo;
private Queue<Integer> queue;
private boolean[] onQueue;
public BellmanFordSP(EdgeWeightedDigraph G, int s) {
distTo = new double[G.V()];
onQueue = new boolean[G.V()];
edgeTo = new DirectedEdge[G.V()];
for (int v = 0; v < G.V(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
distTo[s] = 0.0;
queue = new Queue<>();
queue.enqueue(s);
onQueue[s] = true;
while (!queue.isEmpty()) {
int v = queue.dequeue();
onQueue[v] = false;
relax(G, v);
}
}
private void relax(EdgeWeightedDigraph G, int v) {
for (DirectedEdge e : G.adj(v)) {
int w = e.to();
if (distTo[w] > distTo[v] + e.weight()) {
distTo[w] = distTo[v] + e.weight();
edgeTo[w] = e;
if (!onQueue[w]) {
queue.enqueue(w);
onQueue[w] = true;
}
}
}
}
public Iterable<DirectedEdge> pathTo(int v) {
Stack<DirectedEdge> path = new Stack<>();
for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()])
path.push(e);
return path;
}
}
Single source shortest-path implementation: cost summary
| algorithm | restriction | typical case | worst case | extra case |
|---|---|---|---|---|
| topological sort | no directed cycles | E + V | E + V | V |
| Dijkstra (binary heap) | no negative weights | ElogV | ElogV | V |
| Bellman-Ford | no negative cycles | EV | EV | V |
| Bellman-Ford(queue-based) | no negative cycles | E + V | EV | V |
4.4.1
True or false. Adding a constant to every edge weight does not change the solution to the single-source shortest-paths problem.
False. 假设一条最短路径的长度是15, 且一共有五条边,而另外一条简单路径的长度为20,由两条边组成,当每条边的权值都增加5之后,原来长度15的路径长度变为40,原来长度为20的路径长度变为30,可以看到最短路径改变了。
4.4.5
Change the direction of edge 0->2 in tinyEWD.txt (see page 644). Draw two different
SPTs that are rooted at 2 for this modified edge-weighted digraph.
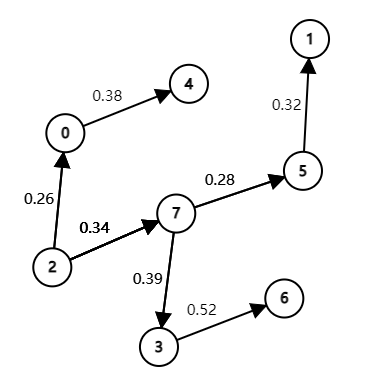
4.5.9
The table below, from an old published road map, purports to give the length of the shortest routes connecting the cities. It contains an error. Correct the table. Also, add a table that shows how to achieve the shortest routes.
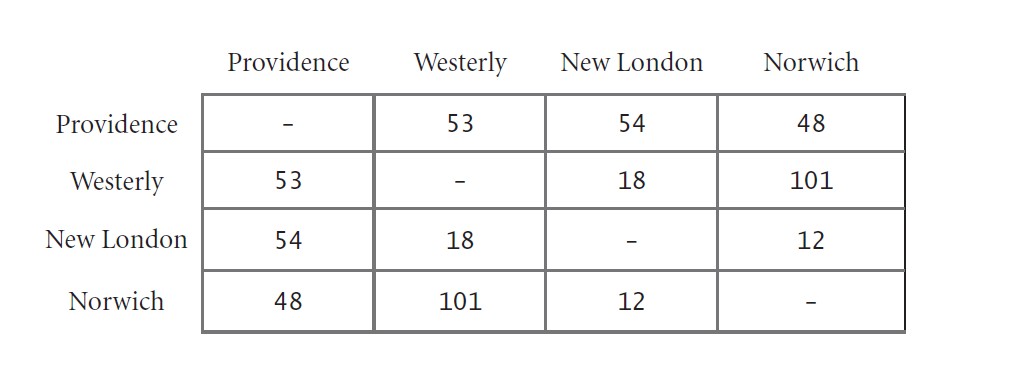
| Providence | Westerly | New London | Norwich | |
|---|---|---|---|---|
| Providence | 53 | 54 | 48 | |
| Westerly | 53 | 18 | 30 | |
| New London | 54 | 18 | 12 | |
| Norwich | 48 | 30 | 12 |
给Providence、Westerly、New London、Norwich 分别编号为0、1、2、3
最短路径:
| Providence | Westerly | New London | Norwich | |
|---|---|---|---|---|
| Providence | 0-1 | 0-2 | 0-3 | |
| Westerly | 1-0 | 1-2 | 1-2、2-3 | |
| New London | 2-0 | 2-1 | 2-3 | |
| Norwich | 3-0 | 3-2、2-1 | 3-2 |
String sorts
key-indexed counting
Proposition. Key-indexed counting uses $ ~ 11N+4R $ array accesses to sort a N items whose keys are integers between 0 and R-1.
Proposition. Key-indexed counting uses extra space proportional to N + R
Stable.
public class CountingSort {
public static void sort(int[] a, int R) {
int N = a.length;
int[] count = new int[R+1];
int[] aux = new int[N];
for (int i = 0; i < N; i++)
count[a[i]+1]++; // count[a[i]+1] = count[a[i+1]] + 1
for (int r = 0; r < R; r++)
count[r+1] += count[r]; // 第一个位置
for (int i = 0; i < N; i++)
aux[count[a[i]]++] = a[i]; // aux[count[a[i]] = count[a[i]]+1] = a[i]
for (int i = 0; i < N; i++)
a[i] = aux[i];
}
public static void main(String[] args) {
String s = "dacffbdbfbea";
int[] a = new int[s.length()];
for (int i = 0; i < a.length; i++)
a[i] = s.charAt(i)-'a';
sort(a, 26);
for (var e : a) {
System.out.printf("%c ", e+'a');
}
}
}
LSD radix sort
Least-significant-digit-first string sort
- Consider characters from right to left.
- Stably sort using dth character as the key (using key-indexed counting).
public class LSD {
public static void sort(String[] a, int W) {
int R = 256;
int N = a.length;
String[] aux = new String[N];
for (int d = W-1; d >= 0; d--) {
int[] count = new int[R+1];
for (int i = 0; i < N; i++)
count[a[i].charAt(d)+1]++;
for (int r = 0; r < R; r++)
count[r+1] += count[r];
for (int i = 0; i < N; i++)
aux[count[a[i].charAt(d)]++] = a[i];
for (int i = 0; i < N; i++)
a[i] = aux[i];
}
}
public static void main(String[] args) {
In in = new In("D:\\Java_test\\test1\\src\\StringSort\\strings.txt");
String[] a = in.readAllStrings();
int N = a.length;
int w = a[0].length();
for (int i = 1; i < N; i++)
assert a[i].length() == w : "String must have fixed length";
sort(a, w);
for (var e : a)
System.out.println(e);
}
}
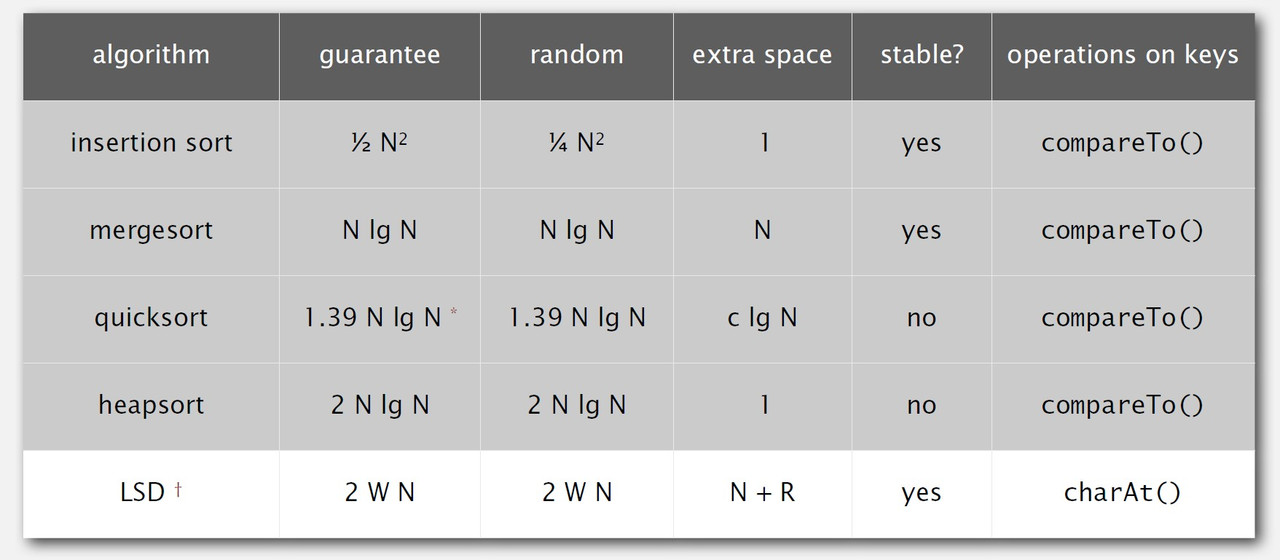
Summary of the performence of sorting algorithms
MSD radix sort
Most-significant-digit-first srting sort
- Partition array into R pieces according to first character (using key-indexed counting).
- Recursively sort all strings that start with each character (key-indexed counts delineate subarrays to sort).
Implementation
public class MSD {
final static int R = 256;
public static void sort(String[] a) {
String[] aux = new String[a.length];
sort(a, aux, 0, a.length-1, 0);
}
private static void sort(String[] a, String[] aux, int lo, int hi, int d) {
if (hi <= lo) return;
int[] count = new int[R+2];
for (int i = lo; i <= hi; i++)
count[charAt(a[i], d)+2]++;
for (int r = 0; r < R + 1; r++)
count[r+1] += count[r];
for (int i = lo; i <= hi; i++)
aux[count[charAt(a[i], d)+1]++] = a[i];
for (int i = lo; i <= hi; i++)
a[i] = aux[i - lo];
for (int r = 0; r < R; r++)
sort(a, aux, lo+count[r], lo+count[r+1]-1, d+1);
}
private static int charAt(String s, int d) {
if (s.length() > d) return s.charAt(d);
else return -1;
}
public static void main(String[] args) {
In in = new In("D:\\Java_test\\test1\\src\\StringSort\\strings.txt");
String[] a = in.readAllStrings();
sort(a);
for (var e : a)
System.out.println(e);
}
}
suffix arrays
Longest repeated substring: Java implementation
public class LRS {
public static String lrs(String s) {
int N = s.length();
String[] suffixes = new String[N];
for (int i = 0; i < N; i++)
suffixes[i] = s.substring(i, N);
Arrays.sort(suffixes);
String lrs = "";
for (int i = 0; i < N - 1; i++) {
int len = lcp(suffixes[i], suffixes[i+1]);
if (len > lrs.length())
lrs = suffixes[i].substring(0, len);
}
return lrs;
}
private static int lcp(String s, String t) {
int n = Math.min(s.length(), t.length());
for (int i = 0; i < n; i++)
if (s.charAt(i) != t.charAt(i)) return i;
return n;
}
public static void main(String[] args) {
String s = "aacaagtttacaagc";
System.out.println(lrs(s));
}
}