理论

  1. 在之前的教程中，我们学习了如何使用Sobel算子。它是基于这样一个事实，即在边缘区域，像素强度显示了一个 “跳跃"或强度的高变化。得到强度的一阶导数，我们观察到边缘的特征是一个最大值，如图所示：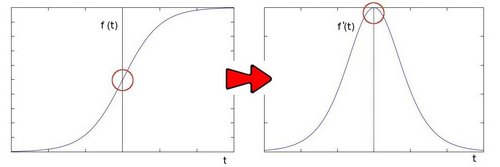

  2. 那么，如果我们取二阶导数会怎样？

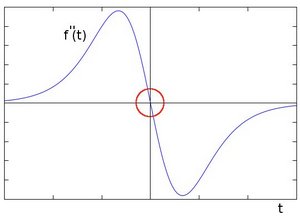    你可以观察到，边缘二阶导数是零! 因此，我们也可以用这个标准来尝试检测图像的边缘。然而，请注意，零值不仅会出现在边缘（它们实际上可以出现在其他无意义的位置）；这可以通过在需要时使用过滤来解决。

拉普拉斯算子

  1. 从上面的解释中，我们可以推断出，二阶导数可以用来检测边缘。由于图像是二维的，我们需要在两个维度上取导数。这里，拉普拉斯算子就派上用场了。 拉普拉斯算子的定义是： $$ Laplace(f) = \frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2} $$
  2. 拉普拉斯算子在OpenCV中是由函数Laplacian()实现的。事实上，由于拉普拉斯算子使用图像的梯度，它在内部调用索贝尔算子来进行计算的。

Code

代码链接

Explanation

变量声明

// Declare the variables we are going to use
Mat src, src_gray, dst;
int kernel_size = 3;
int scale = 1;
int delta = 0;
int ddepth = CV_16S;
const char* window_name = "Laplace Demo";

加载图像

const char* imageName = argc >=2 ? argv[1] : "./images/lena.jpg";
src = imread( samples::findFile( imageName ), IMREAD_COLOR ); // Load an image
// Check if image is loaded fine
if(src.empty()){
    printf(" Error opening image\n");
    printf(" Program Arguments: [image_name -- default lena.jpg] \n");
    return -1;
}

消除噪声

// Reduce noise by blurring with a Gaussian filter ( kernel size = 3 )
GaussianBlur( src, src, Size(3, 3), 0, 0, BORDER_DEFAULT );

灰度化

cvtColor( src, src_gray, COLOR_BGR2GRAY ); // Convert the image to grayscale

拉普拉斯算子

Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT );
  • 参数如下。
    • src_gray：输入的图像。
    • dst：目标图像
    • ddepth。目的图像的深度。由于我们的输入是CV_8U，我们定义ddepth = CV_16S以避免溢出。
    • kernel_size。内部应用的Sobel算子的核大小。在这个例子中我们使用3。
    • scale, delta 和 BORDER_DEFAULT：我们把它们作为默认值。

将输出转换为CV_8U图像

// converting back to CV_8U
convertScaleAbs( dst, abs_dst );

结果

  1. 编译完上面的代码后，我们可以运行它，并将图像的路径作为参数。例如，以下图输入为例：

  2. 我们得到以下结果。注意到树木和牛的轮廓是如何被近似地定义的（除了在强度非常相似的区域，即牛头周围）。另外，请注意，树木后面的房子的屋顶（右侧）是不明显的标记。这是由于该区域的对比度较高。

References

https://docs.opencv.org/4.5.5/d5/db5/tutorial_laplace_operator.html