理论

  1. 在之前的两个教程中，我们已经看到了卷积的应用实例。最重要的卷积之一是计算图像中的导数（或对它们的近似值）

  2. 为什么图像中的导数计算可能是重要的？让我们设想一下，我们要检测图像中存在的边缘。比如说：

    你可以很容易地注意到，在一个边缘，像素强度的变化是很明显的。一个表达变化的好方法是使用导数。梯度的高变化表示图像中的一个重大变化。

  3. 为了更加形象，让我们假设我们有一个一维图像。在下面的图中，一个边缘由强度的 “跳跃 “来表示：

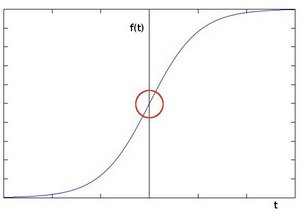
  4. 如果我们取第一个导数，可以更容易地看到边缘的 “跳跃”（实际上，这里出现的是一个最大值）：

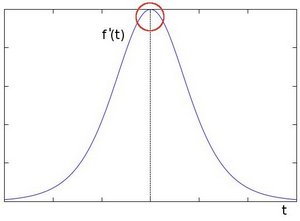
  5. 因此，从上面的解释中，我们可以推断出，检测图像中的边缘的方法可以通过定位梯度高于其邻居的像素位置（或者概括地说，高于一个阈值）来进行。

  6. 更详细的解释，请参考Bradski和Kaehler的《Learning OpenCV》。

Sobel 算子

  1. Sobel算子是一个离散的微分算子，它计算图像强度函数的梯度的近似值。
  2. Sobel算子结合了Gaussian smoothing和微分。

Formulation

假设要操作的图像为 $I$:

  1. 我们计算两个导数：
    1. 水平变化：这是通过用奇数大小的内核 $G_x$ 对 $I$ 进行卷积计算的。例如，对于内核大小为 $3$ ， $G_x$ 将被计算为： $$ G_x=\begin{bmatrix} -1 & 0 & +1\\ -2 & 0 & +2\\ -1 & 0 & +1 \end{bmatrix} * I $$
    2. 垂直变化：这是通过用奇数大小的内核 $G_y$ 对 $I$ 进行卷积计算的。例如，对于内核大小为 $3$ ， $G_y$ 将被计算为： $$ G_y = \begin{bmatrix} -1 & -2 & -1\\ 0 & 0 & 0\\ +1 & +2 & + 1 \end{bmatrix} * I $$
  2. 在图像的每一点上，我们通过结合上述两个结果计算出该点的梯度近似值： $$ G = \sqrt{G_{x}^{2}+G_{y}^{2}} $$ 有时会使用以下更简单的方程式： $$ G = |G_x|+|G_y| $$

当核的大小为 $3$ 时，上面显示的 Sobel核可能会产生明显的不准确（毕竟， Sobel 只是一个导数的近似值）。OpenCV通过使用 Scharr() 函数来解决这种大小为 $3$ 的核的不精确性。这和标准的 Sobel 函数一样快，但比它更准确。它可以实现以下内核 $$ G_x=\begin{bmatrix} -3 & 0 & +3\\ -10 & 0 & +10\\ -3 & 0 & +3 \end{bmatrix}, G_y=\begin{bmatrix} -3 & -10 & -3\\ 0 & 0 & 0\\ +3 & +10 & +3 \end{bmatrix} $$

Code

代码链接

Explanation

变量声明

// First we declare the variables we are going to use
Mat image,src, src_gray;
Mat grad;
const String window_name = "Sobel Demo - Simple Edge Detector";
int ksize = parser.get<int>("ksize");
int scale = parser.get<int>("scale");
int delta = parser.get<int>("delta");
int ddepth = CV_16S;

加载图像

String imageName = parser.get<String>("@input");
// As usual we load our source image (src)
image = imread( samples::findFile( imageName ), IMREAD_COLOR ); // Load an image
// Check if image is loaded fine
if( image.empty() )
{
  printf("Error opening image: %s\n", imageName.c_str());
  return EXIT_FAILURE;
}

消除噪声

// Remove noise by blurring with a Gaussian filter ( kernel size = 3 )
GaussianBlur(image, src, Size(3, 3), 0, 0, BORDER_DEFAULT);

灰度化

// Convert the image to grayscale
cvtColor(src, src_gray, COLOR_BGR2GRAY);

Sobel 算子

Mat grad_x, grad_y;
Mat abs_grad_x, abs_grad_y;
Sobel(src_gray, grad_x, ddepth, 1, 0, ksize, scale, delta, BORDER_DEFAULT);
Sobel(src_gray, grad_y, ddepth, 0, 1, ksize, scale, delta, BORDER_DEFAULT);
  • 我们计算 $x$ 和 $y$ 方向的 “导数”。为此，我们使用函数Sobel()，如下所示。该函数需要以下参数:
    • src_gray：在我们的例子中，输入的图像。这里是CV_8U
    • grad_x / grad_y：输出图像。
    • ddepth：输出图像的深度。我们将其设置为CV_16S以避免溢出。
    • x_order： $X$ 方向上的导数顺序。
    • y_order: $Y$ 方向的导数顺序。
    • scale：delta和BORDER_DEFAULT：我们使用默认值。

注意，在计算 $x$ 方向的梯度时，我们使用：xorder=1，yorder=0，我们对 $y$ 方向进行类似的计算。

转换为CV_8U图像

// converting back to CV_8U
convertScaleAbs(grad_x, abs_grad_x);
convertScaleAbs(grad_y, abs_grad_y);

梯度

addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad);

我们试图通过增加两个方向的梯度来近似计算梯度（注意，这不是一个精确的计算！但对我们的目的来说是好的）。

结果

References

https://docs.opencv.org/4.5.5/d2/d2c/tutorial_sobel_derivatives.html